
Edward Winter

Illustration from Das leidenschaftliche Spiel by Gustav Schenk (Bremen, 1936)
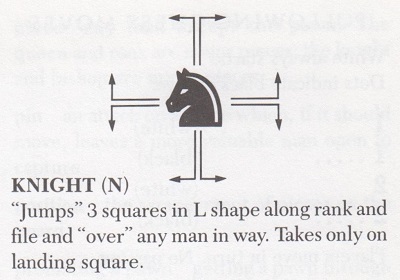
How does the knight move? Or, rather, how can the knight’s move be described succinctly? Innumerable formulations have been proposed, but where is the ‘perfect’ definition? Readers are invited to try their hand, and for general guidance a sample of some of the old-timers’ efforts is offered.
‘The knights move obliquely, backward or forward, upon every third square, including that which they stood on, from black to white, and from white to black …’ Stratagems of Chess (1817), pages 3-4.
‘The knight moves obliquely, from the square it stands on to that of a different colour two squares distant.’ An Easy Introduction to the Game of Chess (1820), page 2.
‘The knight moves one square forward, backward or sideway; and finishes the move by proceeding one square diagonally; or, the knight may be moved at first one square diagonally, and then one square forward or sideway.’ A New Treatise on Chess by G. Walker (1833), page 3.
‘The knight’s line of motion and attack is along the diagonals of parallelograms, 3 by 2, in every direction to the opposite square.’ Chess Player’s Chronicle (1842), page 383. After quoting this definition in the introduction to unit three of Napier’s Amenities and Background of Chess-Play, W.E. Napier remarked: ‘Lately, I heard a better definition, jocularly spoken by a lady-pupil of mine. It owes nothing to Euclid or to Blackstone, but much to human nature. Said she, “The knight-leap is as close as two jealous queens can be, without mischief to either”.’
‘The move of the knight consists of the shortest rook’s move and the shortest bishop’s move, both at once.’ Amusements in Chess by C. Tomlinson (1845), page 154.
‘When placed on any square towards the middle of the board, he cannot move to either of the eight squares which are contiguous to that on which he stands; but he may be played to any of an opposite colour to that which he then occupies, of the 16 squares which surround those eight.’ Introduction to The Chess Player’s Magazine (1846-47), page 8.
‘His move is one square in a straight line, and one in an oblique direction ...’ The Chess-Player’s Handbook by H. Staunton (1847), page 5.
‘It has a zigzag or oblique motion, leaping over an adjoining square to a square of a different colour from that from which it started.’ The Manual of Chess by C. Kenny (New York, 1859), pages 31-32.
‘The knights have a peculiar oblique move of their own. The knight can move over another piece three squares at a time; that is, he leaps from the square he stands on – passes over another – and rests on the third.’ A Handbook of Chess by G. F. Pardon (1860), pages 9-10.
‘The knight’s move is one square in a straight line, and one in an oblique direction.’ The ABC of Chess by A Lady (circa 1860), page 8.
‘The knight’s move is simply two squares of the rook’s move, and then one square at right angles, finishing on the last-mentioned, and having power over it alone.’ The Book of Chess by G.H. Selkirk (1868), page 27.
‘His leap carries him over one square in a straight line to one in an oblique direction. But this peculiarity will be better understood by an attentive study of the annexed diagram, and very much more readily by the tuition of some chess-playing acquaintance.’ The Laws and Practice of Chess by H. Staunton and R. Wormald (1876), page 36.
‘He moves or captures from the square where he stands to any third square of an opposite colour to the one from which he started, by skipping one diagonal square and then landing on the next square of the same line or row, or vice versa.’ The Modern Chess Instructor by W. Steinitz (1889), page xiv.
‘The knight may move in any direction to the square next but one of a different colour from that on which it stands; or in other words, may move horizontally or vertically in either direction, two squares forward and then one square to either right or left. … The knight’s move forms the diagonal of a parallelogram of three squares by two.’ Chess by R.F. Green (1889), pages 8-9.
‘The move is from a black square to a white, or from a white square to a black, round the corner, traversing one square diagonally to the next straightforwards; or one square straightforwards to the next diagonally.’ Chess for Beginners and the Beginnings of Chess by R.B. Swinton (1891), pages 11-12.
‘One move of the knight combines two king’s moves: one square straight, and one square diagonally to any but the adjoining squares to its starting-point.’ Chess by L. Hoffer (various editions, as from 1892).
‘The knight’s distance is limited to two squares, and his direction is intermediate between the rectangular one of the rook and the diagonal one of the bishop. … Mathematically considered, the knight’s move is in the diagonal of a rectangle of six squares or points …’ The Principles of Chess in Theory and Practice by J. Mason (various editions from 1894), page 9.
‘We now come to the knight, which radiates its force in the directions of obliques; and as the length of an oblique … is fixed and invariable, the magnitude of the force exerted by the knight in any one direction is also fixed and invariable: that is, the knight commands only one point in any one direction, that point being the final point of the oblique of which the position of the knight is the initial point.’ The Minor Tactics of Chess by F.K. Young and E.C. Howell (1895), page 31.
‘A square is said to be “commanded”… by a knight when that square and the square on which the knight stands are corner squares of a rectangle consisting of six squares in two rows of three each, such corner squares not being of the same rank or file.’ Everybody’s Guide to Chess and Draughts by H. Peachey (1896), page 16.
‘The knight has a very peculiar movement, going always two squares along a row or file, and then changing the colour of the square he stands upon by going off at a right angle, one square to the right or left.’ Chess A Manual for Beginners by R.F. Foster (1897), page 23.
‘The knight, whose movement differs materially from that of the other pieces, and who moves one square forward and one square obliquely, or one square obliquely and one square forward, combining the action of the rook and bishop, …’ The Chess-Player’s Manual by G.H.D. Gossip (edition revised by S. Lipschütz, 1902), page 8.
‘He changes the colour of his square every time. He moves two squares in a line with the one he is on and then one sideways.’ “Popular” Handbook of Chess by Professor de Lyons Pike (circa 1902), page 7.
‘It goes two squares in any direction upon rank or file, and then one square to right or left (upon rank or file).’ A Handbook of Chess by W. Chinn (1907), page 9.
‘One square, as a rook moves, then one square as a bishop (in any further direction); in moving he changes rank, file, diagonal, and colour of square.’ The Modern Chess Primer by E.E. Cunnington (seventh edition, 1913), page 9.
‘The knight moves in a peculiar way, viz., one square diagonally and then one square forwards, backwards or sideways, or vice versa, one square forwards or backwards or laterally and one square diagonally. His move combines the action of the shortest move of the bishop and the shortest move of the rook, or vice versa.’ The Complete Chess-Guide by F.J. Lee and G.H.D. Gossip (1914 edition), page 4.
‘He moves in a zig-zag, two squares one way and then one square to either side.’ Chess: An Easy Game by A.W. Foster and R.E. Kemp (1914), page 2.
‘The knight plays and captures alternately on white and black squares, and only reaches such squares as are nearest to him without being immediately adjacent; his move is as it were composed of two steps, one square in a straight line, and one in an oblique direction.’ Chess Strategy by Ed. Lasker (1915), page 2.
‘A square is commanded by … a knight, when that square and the square on which the knight is standing are as near to each other as, without being of the same rank or file or diagonal, it is possible for two squares to be.’ Revised draft of the American Chess Code (American Chess Bulletin, March 1917, page 53).
‘The knight’s move is perhaps best described as a leap to the next but one square of different color’. Chess and Checkers The Way to Mastership by Ed. Lasker (1918), page 10. A footnote was added: ‘It may be helpful to consider the knight’s move when completed as having described a letter “L” composed of four squares, three in one direction and one at right angles to them.’
‘The knight does move two squares distant, but one is on the straight and one diagonal.’ Chess: Draughts: How to enjoy them by C. Platt (1933), page 21.
‘The knight can play upon any opposite-coloured square that is two squares away from him. There is an ingenious description of his powers which runs thus: consider him to be situated in one corner of a box of three squares by two squares. He can play into the opposite corner of this box.’ Chess for the Fun of It by B. Harley (1933), page 10.
‘The move can be said to consist of a double move, first moving one square in the manner of a rook and then one square in that of a bishop, but always away from the starting-point.’ A Breviary of Chess by S. Tartakower (1937), page 15. The original text, on pages 18-19 of Bréviaire des échecs (Paris, 1934): ‘Sa marche, baroque à première vue, consiste à faire de petits sauts avec changement continuel de la couleur de la case occupée. En décomposant sa marche, on peut dire qu’il franchit d’abord une case comme la Tour, ensuite une case comme le Fou (ou vice-versa), en s’éloignant toujours de la case de départ.’
‘The knight moves in an odd manner. It moves one square vertically or horizontally and then one square diagonally.’ Jaffe’s Chess Primer by C. Jaffe (1937), page 15. On its own (i.e. without the example that Jaffe subsequently gave) this description would mean that a knight on g1 could move to g2. This drawback, which applies to various other definitions quoted here, was also pointed out by D.J. Morgan on page 136 of the May 1953 BCM.
‘Either he goes forward one square and then one square diagonally to the right or left, or he goes immediately to a diagonally right or left square and then forward one square.’ Chess in an Hour by F.J. Marshall (1937/1944), page 21.
The above citations were given by us in an article at the Chess Café in 1998.
C.N. 4693 mentioned that page 3 of Across the Board: The Mathematics of Chessboard Problems by John J. Watkins (Princeton and Oxford, 2004) offered a simple wording which may be better than any of those quoted above:
In C.N. 5096 Jon Crumiller (Princeton, NJ, USA) gave the following pre-nineteenth-century examples:
Our correspondent mentioned too that the description quoted above from Stratagems of Chess (1817) is a word-for-word copy from page 117 of Hoyle’s Games Improved (1800) and that a very similar text occurs on page 88 of R. Lambe’s The History of Chess (1764):
‘The Knights move obliquely, stepping upon every third square, including that which they quit; from black to white, and from white to black, over the heads of men, which none else do.’
We note a similar wording on page 20 of Chess Made Easy by J.A. Guthrie (London, 1922):
‘The Knights move obliquely upon every third square, Black to White and White to Black.’
In C.N. 5132 Pablo S. Domínguez (Madrid) pointed out Emanuel Lasker’s unusual explanation which appeared on pages 5-6 of Lasker’s Manual of Chess (New York, 1927), as well as in later editions of the book:
‘... the knight jumps in making the shortest move that is not a straight one.’
The corresponding text in the earlier German edition, Lehrbuch des Schachspiels, reads:
‘... der Springer macht einen Sprung, nämlich den kürzesten auf dem Schachbrett möglichen Zug, der nicht gerade ist.’
The English volume (page 10) also had this description of the knight’s move:
‘The shortest jump on the chess board is, namely, to take two squares (in the air) in a line or row and one square perpendicularly thereto.’
Another curiosity, on pages 25-26 of Learn Chess Fast! by S. Reshevsky and F. Reinfeld (various editions), is the presentation of the knight’s move in the captions to diagrams 50-53:


Have many other instructional works explained the knight’s move in this way, i.e. by reference to squares inaccessible to the queen?
(8431)
C.N. 8431 asked whether many instructional works had explained the knight’s move by reference to squares inaccessible to the queen, as did Learn Chess Fast! by S. Reshevsky and F. Reinfeld.
Trevor Moore (Baughurst, England) draws attention to Chess by C.H.O’D. Alexander (London, 1937), as well as the expanded, updated edition, Alexander on Chess (London, 1974). From pages 4-5 of both books:
‘Like the other pieces it [the knight] moves in a straight line, but one less clearly indicated on the board than those of the rook and bishop. The rook moves parallel to the edges of the board, the bishops diagonally and the knight in a direction bisecting the angle between the rook’s and bishop’s move. ... The knight’s move is complementary to that of the queen, as we may easily see in the following way. Place the queen on one of the 16 central squares of the board – it controls 16 of the 24 squares surrounding it. Now place a knight on the square instead – it controls precisely those eight squares not attacked by the queen. ... It is often inaccurately said that the knight “jumps” other pieces – actually, it simply moves between them.’
(8465)
A similar point about the knight was made on page 4 of Learn Chess: A New Way for All by C.H.O’D. Alexander and T.J. Beach (Oxford, 1963):
‘It is not obstructed by pieces of either colour, since moving across the two by three box it passes between them.’
(8502)
A further citation is FIDE’s definition of the knight’s move, which Sven Mühlenhaus (Düsseldorf, Germany) appreciates for its concision:
‘The knight may move to one of the squares nearest to that on which it stands but not on the same rank, file or diagonal.’
(8454)
‘The knights move in a letter L one square orthogonally in one direction and then two squares orthogonally at right angles to the first move, or two squares orthogonally in one direction and then one square at right angles to it.’
Source: Page 11 of the original (Aylesbury, 1976) edition of Discovering Chess by R.C. Bell (‘R.C. Bell MB FRCS’).
(8460)
From Robert John McCrary (Columbia, SC, USA):
‘The “American Chess Code”, published in 1897 and the same as the “British Chess Code” published shortly beforehand, contains on page 24 the earliest official definition of a knight’s move in a Code that I have seen. It states that a square is commanded by a knight ...
“... when that square and the square on which the knight stands are as near to each other as, without being of the same rank or file or diagonal, it is possible for two squares to be ...”This appears to be an official definition that is essentially the same as saying that the knight moves to the nearest square that cannot be commanded by a queen.’
We add another explanation of the knight’s move, from page 19 of First Book of Chess by I.A. Horowitz and Fred Reinfeld (New York, 1952):
‘“The old one-two” is the phrase that aptly describes the knight’s move. Each knight move is a combination of one square and two squares:
(a) one square “North” or “South”; then two squares “East” or “West”.
(b) one square “East” or “West”; then two squares “North” or “South”.’
(8532)
From page 14 of An Invitation to Chess by Irving Chernev and Kenneth Harkness (New York, 1945):
‘The knight jumps over friendly or enemy pieces. It leaps one square (to the North, South, East or West) and lands to the right or to the left on a square of the opposite color to the one from which it started.’
The explanation on page 8 of Chess Self-Teacher by Al Horowitz (New York, 1961):
‘The knight has a peculiar move, best described as “to the nearest square of opposite color that is not adjacent”. He moves in the shape of an inverted L.’
‘The simplest way to consider the knight’s move is to imagine a three-square L-shape. The basic L-shape is achieved by moving the knight two squares in any direction and then one square to either side.
This L-shape can also be achieved by imagining the short side of the “L” being played first. Move the knight one square in any direction, and then two squares to either side.’
Source: page 31 of Chess for Rookies by Craig Pritchett (London, 2009).
Above there is a line from page 154 of Amusements in Chess by Charles Tomlinson (London, 1845): ‘The move of the knight consists of the shortest rook’s move and the shortest bishop’s move, both at once.’
A similar remark was on page 47, alongside a more complex explanation:
‘Geometrically, the knight’s leap is always the hypothenuse of a right-angle triangle, of which the base equals twice the perpendicular, the latter being equal to the side of one square.’

Tomlinson’s text was originally published on page 191 of the Saturday Magazine, 13 November 1841.
From page 29 of Amusements in Chess:
(9576)

Bruce Monson (Colorado Springs, CO, USA) has pointed out an article, ‘The Mysterious Knight Move’, on pages 30-33 of the February 2015 Mensa Bulletin, and we are grateful to the writer, Frank Camaratta (Huntsville, AL, USA), for permission to reproduce extracts:

Diagram 3 showed how the ‘primordial bishop, or al-fil, ... has the ability to jump one square diagonally in any direction. It does not control the intervening square, nor can it be obstructed’, and Mr Camaratta then commented, in connection with Diagram 4 (showing a rook): ‘Logically then, there must have been, at least in the embryonic forms of chess, a piece that “jumped” like the bishop but horizontally and vertically rather than diagonally.’

(9625)
Further to mention of the letter L in explanations of the knight’s move, it is worth adding that Russian-language sources often refer to the Г, as in the word Гамбит. A passage from page 7 of The Life and Games of Mikhail Tal (New York, 1976):

The text is on page 17 of the London, 1997 edition.
(9631)
From page 27 of “Among These Mates” by Chielamangus (Sydney, 1939):
‘The knight’s move is very puzzling. It moves there and then there, or the same only backwards or sideways, and really all round.’
In the description of knights on page 11 of Easy Guide to the Game of Chess by Charles Check (London, 1818):
‘They move in a peculiar way in any direction; leaping from the square in which they stand, over either of the contiguous squares, into one of the two that have a corner in contact with one of the farther corners of the square over which they leap.’
From page 7 of Practical Chess Grammar by W.S. Kenny (London, 1817):
‘The knight has a peculiar way of moving, entirely different from any other piece on the board, in a direction partly diagonal and partly straight. His march is oblique, upon every third square, including that which he stood on, from black to white, and from white to black, over the heads of the men, which no other is allowed to do.’

Source: Chess Amateur, July 1912, page 673.
(10215)
A particularly poor description on page 121 of Chess for Children by Ted Nottingham, Bob Wade and Al Lawrence (New York, 1993 and 1996):
Michael McDowell (Westcliff-on-sea, England) writes:
‘Fairy chess enthusiasts divide pieces into riders, leapers and hoppers, although this does not by any means cover all unorthodox pieces. Riders can move any distance along a line unless obstructed (e.g. bishop, rook, queen), leapers move directly to a square ignoring any obstacle, and hoppers need a hurdle to jump over in order to move. Hence the knight is succinctly described as a 2,1 leaper. There are numerous unorthodox examples, such as the camel (a 3,1 leaper) and the root-50 leaper (which combines two lengths of move, being a 5,5 or 7,1 leaper).’
Our correspondent furthermore draws attention to the definitions on pages 8-9 of A Guide to Fairy Chess by Anthony Dickins (Richmond, 1969 and New York, 1971). The first edition was published in Richmond in 1967.
(11132)
Fabrizio Zavatarelli (Milan, Italy) draws attention to this excerpt from the ninth edition of the Encyclopaedia Britannica, on page 593:

The article on chess, published in the mid-1870s, was signed ‘W.N.P.’, i.e. William Norwood Potter. His obituary on page 180 of the April 1895 BCM called it ‘masterly’; page 226 of the April 1895 Chess Monthly stated that Potter edited the article ‘together with Steinitz and Zukertort’.
(11263)
From page 136 of the May 1953 BCM, in D.J. Morgan’s Quotes and Queries column:

The exact wording in A.F. Mackenzie’s book:

That comes from the section entitled ‘The Elements of Chess’. The full explanation of the knight’s move (pages 12-14, with three diagrams) left no ambiguity.
(11421)

A History of Chess by H.J.R. Murray (Oxford, 1913)

Great Moments in Chess by F. Reinfeld (New York, 1963)
From page 5 of The Game of Chess by Edward Lasker (New York, 1972):
‘... he goes to any of the nearest squares of opposite color which are not next to him.’
An extract from an article about the knight by W.H. Cozens on pages 22-25 of Games & Puzzles, January 1976:
‘It is curious that the writers of so many beginners’ books find difficulty in defining the knight’s move. “One along and one diagonally” and “Two up and one across” are two nonsensical efforts ...
The easiest definition of the knight move is: on a block of squares 3 x 2 a knight jumps from one corner to the diagonally opposite corner.’
Another indispensable entry in B.J. Horton’s Dictionary of Modern Chess:
‘HIPPOPHOBIA: A term sometimes applied to chessplayers who dread the presence of knights on the chessboard ... Chessplayers who are afflicted with hippophobia are known to take great risks so as to eliminate their opponents’ knights.’
Horton names no names.
We also like the entry ‘MIDSUMMER MADNESS’: ‘An expression used by the editor of The Field when he referred to Steinitz’s 20th move (20...P-KN4) as “midsummer madness”. No further explanatory comment was given. The game was played between Blackburne and Steinitz in a Vienna tournament.’
It is hard to know what to make of this drivel. But of course the whole affair is devoid of importance, ‘midsummer madness’ being no more worth knowing than ‘hippophobia’.
If our thinking is not too tortuous, Horton makes Sunnucks look like Murray.
(530)
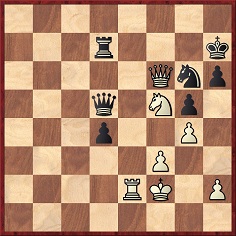
Our above-mentioned Chess Café article (1998) concluded with examples of the knight fork, the first of which arose after a blunder by Black:

H. Fahrni-B. Kostić, Carlsbad, 12 September 1911
Black played 34…Qe6 and resigned after 35 Qxh7+ Kxh7 36 Ng5+ Kg6 37 Nxe6. His remaining three pieces are forked.
Source: volume 2 of the tournament book, pages 59-60.
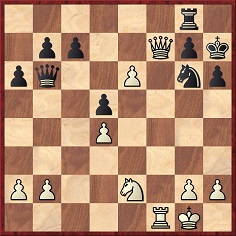
G. MacDonnell-J. Wisker, London, 1876
Here Black erred with 37…d3 and resigned after 38 Re7+ Rxe7 39 Qxg6+.
Source: Deutsche Schachzeitung, June 1876, pages 172-173.
From the Columbia Chess Chronicle, 12 November 1887, page 185:
Constantini-Hruby, Trieste, 1887
25 h4 Nxh4 26 e7 Qg6 27 Qxg8+ Kxg8 28 Rf8+ Kh7 29 Nf4 Nf3+ 30 Kf2 Qc2+ 31 Kxf3 (The Chronicle says that 31 Kg3 ‘was more expeditious’.) 31…Qe4+ 32 Kg3 Qe1+ 33 Kh3 g5 34 Rf7+ Kg8 35 Rf8+ Kg7 36 Nh5+ Kh7 37 Rf7+ Kh8
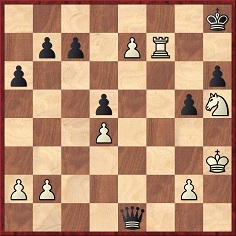
38 e8(Q)+ Qxe8 39 Rh7+ Kxh7 40 Nf6+ Kg6 41 Nxe8 Resigns.
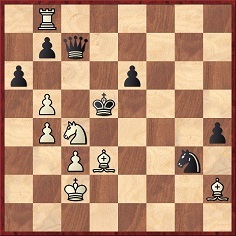
G. Sieg-N.N., Görlitz, 1892
White won by 1 Rxb7 Qxb7 2 Be4+ Kxe4 3 Nd6+. 2…Nxe4 would have allowed a cute mate in one by the knight.
Source: Deutsche Schachzeitung, April 1892, page 119.
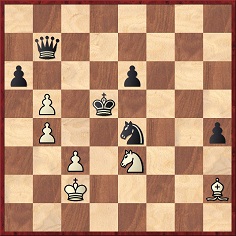
The variation 2...Nxe4 3 Ne3 mate
Another knight fork, after a blunder by White, occurred in a game between Sir George Thomas and William Winter (London, 12 October 1927), as given in C.N. 494.
C.N. 2370 (see page 162 of A Chess Omnibus) commented that many beginners’ books, especially from the United States, give the advice ‘A knight on the rim is grim’. As an addition we suggested: ‘A knight in the corner is forlorner.’ A subsequent item (C.N. 6877) mentioned that both ‘grim’ and ‘dim’ are to be found, and that the latter version appeared, in quotation marks, on page 17 of the January 1963 Chess Review and on page 175 of the magazine’s June 1964 issue. In both cases the writer was Al Horowitz.
What more can be discovered about the maxim?
A third possibility, with ‘trim’, was given by William Lombardy on page 121 of the April 1969 Chess Review:
‘Tinsley has said: “Knight on the rim equals trim.”’
Lombardy also quoted the ‘trim’ wording on page 134 of Modern Chess Opening Traps (New York, 1972), adding ‘Tinsley, circa 1880’. On what basis?
On page 237 Lombardy offered a different, anonymous rhyme:
‘A knight on the side one cannot abide’, goes the adage.
That ‘adage’ had been put forward on page 96 of Chess Marches On! by Reuben Fine (New York, 1945), in a note to 26 Qe2 in Lilienthal v Keres, USSR Absolute Championship, 1941:

Such a German text was attributed to Tarrasch on page 77 of Dynamic Chess Strategy by Mihai Şubă (Alkmaar, 2010), in a discussion of the game García Padrón v Şubă, Las Palmas, 1979:

The German observation occurs, in quotation marks, in the unsigned notes to Marco v Taubenhaus, Monte Carlo, 1903, on page 109 of the April 1903 Deutsche Schachzeitung:

(8718)
Pages 25-26 of the Magazine Section of the Sunday Times, 26 November 1961 had an article entitled ‘The Mind of the Russians’ by Lord Taylor, introduced as follows:
‘For generations the Russians have been the great enigma: the Revolution has shrouded their personality still more. Lord Taylor, psychiatrist and politician, here uses the techniques of modern scientific analysis to disentangle their complex make-up.’
Page 26 had this text:

Nowadays, one could expect immediate reports that ‘furious’ readers ‘took to Twitter’ to ‘shut down’ Lord Taylor, but CHESS held back for nearly nine months:

After another long wait, CHESS readers were allowed to chime in, on pages 137-138 of the February 1963 issue. One sentence from the heading:
‘Many letters received, if printed, would have landed us in the law courts.’
The tardy publication of the original feature in CHESS and the heading’s reference to ‘the Sunday Times some weeks ago’ have resulted in Lord Taylor’s article being dated 1962, rather than 1961, by a number of writers. See, for instance, page 43 of Soviet Chess by D.J. Richards (Oxford, 1965).
(11229)
To the Chess Notes main page.
To the Archives for other feature articles.
Copyright: Edward Winter. All rights reserved.