‘Twenty-one players participated.’
‘Suppose that m men played for
Doomshire, and n men played for Gloomshire.
Then we have:
3n/5
+ (100-m)/3 + (2m-2n)/3 = 51
i.e. 5m-n=265 and hence n=5 (m-53).
Now n must be more than 50; m must be greater than n; and (100-m) must
be divisible by three.
Having regard to these considerations, there is only one solution of
the above equation: n=55, m=64.
So 64 men played for Doomshire.’
‘Gambitt should aim at securing nine
points.
There cannot be four others with a
higher score than this; whereas, if Gambitt only scores 8½
points, scores of 9½-9-9-9
are possible.’
‘It is obvious from Mrs Orme’s
comments that the required number is one of four digits, and that
Ronnie has assumed the number to be bacd where in fact it is abcd.
Trial and error does the rest –
facilitated, no doubt, by acquaintance with the theory of numbers.
The numbers are 5760 (24 pairs of
factors) and 7560 (32 pairs of factors) and the Ormes’s number is
7560.’
‘There are 64 letters in the cipher,
which, taken with the chess “problem” is a strong hint that the
cipher depends on a chessboard arrangement. Write the letters,
therefore, in the form of a chessboard, ignoring the division into
“words”. Then draw on transparent paper a chessboard of similar
size and mark the squares referred to in the chess “problem”. Lay
this over the gridded arrangement of letters, and read off the first
16 letters of the message, lying under the marked squares. Now rotate
the diagram through a right angle, and read off the next 16 letters,
and so on until the whole message appears.
The
message is thus shown to be: “Moti Lal preparing attack station with
three thousand Shaitani first April”.’
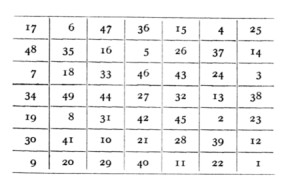
‘The
title and the form of the cryptogram suggest the knight’s move in
chess. The first word is in the bottom right-hand corner, and the
words are picked out according to the following table:
The
question then reads:
“Summa
aetatium Mariae et Annae est quattuor et quadraginta anni. Maria est
bis tantum annorum nata quantum Anna fuit cum Maria fuit dimidio
tantum annorum nata quantum Anna erit cum Anna erit ter tantum
annorum nata quantum Maria fuit cum Maria fuit ter tantum annorum
nata quantum Anna fuit.
Quot
annos nata est Maria?”
This is the old age problem, invented
by Sam Loyd:
“The combined ages of Mary and Ann
are 44 years. Mary is twice as old as Ann was when Mary was half as
old as Ann will be when Ann is three times as old as Mary was when
Mary was three times as old as Ann.
How old is Mary?”
The answer, which can readily be
obtained by simple equations, is that Mary is 27½
and Ann is 16½.’