
Edward Winter

The Patzer, who moved only one pawn, was so mortified by his quick defeat that he burned the score-sheet. Did he burn it enough to disguise how he was mated?
(This puzzle appeared in C.N. 4075, with a clue in C.N. 4084.)
A tough old puzzle from the days of the descriptive notation was given in C.N. 3530 (a clue being added in C.N. 3536):
‘Below is the “score” of a game found in A.D. Brunswick’s rooms after his death under mysterious circumstances. It was in Brunswick’s handwriting. At first it aroused no suspicions, but Inspector Snooper, a keen chessplayer, saw at once that it was some sort of cryptogram.’


‘What was Brunswick’s message?’
Source: pages 28-29 of Caliban’s Problem Book by Hubert Phillips (‘Caliban’), S.T. Shovelton and G. Struan Marshall (London, 1933).
Below is the first in a series of puzzles from C.N.s 3537, 3551 and 3555:
‘The competitors in the Rookwood Chess Congress are organized in two sections. In each section each competitor plays one game against each of the other competitors in that section.
This meant, last year, that the secretary had to arrange 165 games. This year there is one more competitor in each section.
How many games must the secretary arrange?’
Sources: page 198 of Hubert Phillips’s Heptameron (London, 1945) and page 66 of Phillips’ Problem Omnibus Volume 1 (London, 1960).
Source: page 81 and pages 231-232 of Caliban’s Problem Book by Hubert Phillips (‘Caliban’), S.T. Shovelton and G. Struan Marshall (London, 1933).
E) Chess tournament
‘“For the purposes of our chess tournament”, said Woodpusher, “we divided our players into two groups. Each player played two games against each other player in his group. That did away with all possibility of unfairness in regard to the opening move.”
“There must have been a large number of games played altogether.”
“Exactly 200”, said Woodpusher.
How many players in all took part in the tournament?’
Source: Problem Omnibus Volume 1 by H. Phillips (London, 1960), page 73.
F) 100-board match
‘Representatives of Doomshire and Gloomshire met to play chess over 100 boards. Both men and women players took part; each county producing more than 50 men players.
More women played for Gloomshire than for Doomshire.
It was arranged that, so far as possible, men should be matched against men and women against women. This meant that there were only mixed matches (men versus women) to the extent to which the number of men players representing Doomshire exceeded the number of men representing Gloomshire.
On the boards where men were matched against men, Doomshire won three matches out of five. On the boards where women were matched against women, Gloomshire won two matches out of three. And on the boards where Doomshire’s surplus men met Gloomshire’s surplus women, the Doomshire players won two-thirds of the matches. No game ended in a draw. The result was a very narrow win for Doomshire by 51 games to 49.
How many men played for Doomshire?’
Sources: The Hubert Phillips Annual 1951 (London, 1950), page 160 and Problem Omnibus Volume 1 by H. Phillips (London, 1960), page 87.
G) Giuoco Piano
‘“I’m competing”, said Gambitt, “in the Minor Open Reserves at Prawnville.”
“Oh yes? Do you expect to win a prize?”
“Can’t say. There are four prizes altogether.”
“And how many competitors?”
“Twelve. But of course they may divide one or more of the prizes. Scoring is on the usual plan, you see: one point for a win, half a point for a draw. One year all 12 competitors scored five and a half points; the four prizes were divided among them. Last year three competitors tied for first place – they shared the first three prizes – then came three more competitors with equal points; they divided the fourth place. So, you see, there’s always a chance.”
“If I were you, Gambitt”, I said, “I wouldn’t be too ambitious. Aim at scoring just enough points to be certain of at least a share in a prize.”
“Good idea”, said Gambit, “but how many points is that?”
How many points is it?’
Source: Problem Omnibus Volume 1 by H. Phillips (London, 1960), pages 114-115.
‘When Mrs Orme went into the nursery the children were playing with the chessmen.
“What are you doing, dears?”
“Why”, said Ronnie, “Clara and I were talking about our phone number. Clara says it has 32 pairs of factors.”
“So it has”, said Mrs Orme, who had worked that out herself. “But why the chessmen?”
“There are 32 of those”, said Ronnie. “I was putting one back in the box as I worked each pair of factors out. But, Mummy, there’s something wrong. I’ve finished my calculations, and there are still these eight black pawns.”
Mrs Orme took a hasty glance at his notebook. “Ronnie”, she said, “you are a duffer. You’ve got the number wrong.”
“Got the number wrong?” echoed Ronnie.
“Of course. You wouldn’t call yourself Rome, now would you?”
What is the Ormes’s phone number?’
Source: Problem Omnibus Volume 1 by H. Phillips (London, 1960), pages 119-120.
‘During the recent rebellion in Jehannum, a native runner was brought into the small fortified station of Ustaraf, which was occupied by a detachment of the Wellshires, and was found to be carrying in the folds of his pagri a tightly-folded paper, which he gave up without demur. The only writing on it was the following:
Major ffeatherstonehaugh-Haugh, a keen but incompetent chessplayer, who was in command, was greatly interested, and guessed that it must be a chess problem sent to him by Legge-Pullar, who had taught him the rudiments of the game, and whom he knew to be on Intelligence duty somewhere in the interior. He therefore set himself to solve the problem, which seemed to be rather unusual; so unusual, in fact, that three days later he had made nothing of it when another runner was brought in, bearing a paper on which the following was written:
AHAMIT TOT THAR TINALI EFAI ETCHL KRPS SOTTURA EPASTAI APONRR NIWDSIN IHLGT.
Major ffeatherstonehaugh-Haugh regrets he is unable to make head or tail of this, and begs you to translate it for him, as he is not familiar with any Oriental language.’
Source: Caliban’s Problem Book by H. Phillips (‘Caliban’), S.T. Shovelton and G. Struan Marshall (London, 1933), pages 59-60.
‘When I met Professor Graeme Atta the other day he showed me an interesting old manuscript book which he had come across when he was browsing among the second-hand bookstalls in Charing Cross Road. The book plate was almost indecipherable, but as far as I could make out bore the inscription “ex libris Samueli Loyd”. One of the pages contained a curious Latin cryptogram which seems to be of more than passing interest. Here is a copy of it:
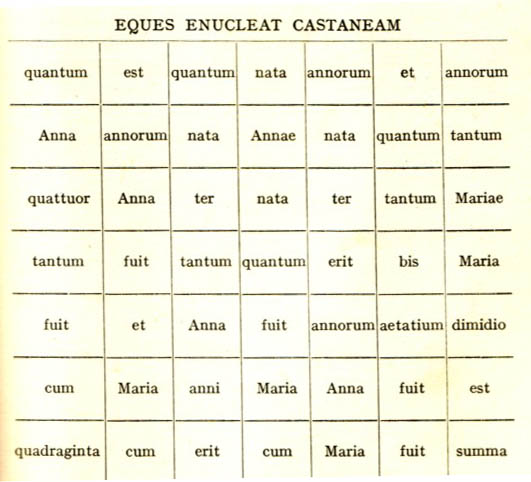
Quot annos nata est Maria?’
Source: Caliban’s Problem Book by H. Phillips (‘Caliban’), S.T. Shovelton and G. Struan Marshall (London, 1933), page 127.
Now, a problem by Sam Loyd given in C.N. 3596:
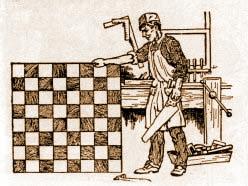
‘This clever young carpenter received a chest of tools for a Christmas present, and immediately set to work to make a fine chessboard to present to Dr Lasker, the chess champion of the world. Dr Lasker is a great mathematician and puzzlist as well as a marvelous chessplayer, but can he beat our puzzlists in discovering the largest number of different pieces that the carpenter could have used in making this board?
Each piece must be made up of squares. One piece can be a single black square, another piece a single white square. Only one piece may consist of two squares, because all two-square pieces are alike. But a three-square piece has four different forms – a straight row with a black square in the middle, a straight row with a white square in the middle, a crooked piece with one black square, and a crooked piece with one white square. When you have divided the checkerboard into the greatest number of pieces, you will have solved the puzzle.’
Finally, a puzzle by Henry Ernest Dudeney, from C.N. 3644:
‘I have a single chessboard and a single set of chessmen. In how many different ways may the men be correctly set up for the beginning of a game? I find that most people slip at a particular point in making the calculation.’
Source: Amusements in Mathematics by H.E. Dudeney (London, 1917), page 105.
All the solutions can be found in the pages of Chess Notes, and a complete list of relevant C.N. items is given under ‘Puzzles’ in our Factfinder. For biographical and other information about Hubert Phillips, see The Chess-loving Puzzle-master. A further problem by him (‘Living-chess puzzle’) appeared on pages 71-72 of Chess Facts and Fables.
The above article originally appeared at ChessBase.com.
A brief paragraph by T.R. Dawson on page 350 of the August 1922 Chess Amateur:
‘Lewis Carroll’s famous “doublet” puzzles, where an initial word is modified into a new word by altering a single letter, and so on step by step to reach a desired final word, are probably known to all readers. A sufficiently illuminating example is the evolution of APE by way of: are, arm, aim, dim, dam, cam, can to MAN. For those who enjoy this kind of thing I propose the following chain: CHESS to CHECK to MATES. It can be done, I have shown crudely – but what is the shortest set of links?’
The ape-man chain given by Dawson is not the quickest route, but he pursued chess-related doublets (which are also known as changelings) in the Chess Amateur from October 1922 to February 1924.
(2520)
A challenge which should not prove too difficult arises from this account of a tournament game which actually appeared in a newspaper:
‘The concluding moves of the game are worth reproducing from the following position: White [identity omitted here], king on king, four pawns on king’s rook, four king’s knights, four king’s bishops, five queen’s bishop, four queen’s knights, three queen’s rooks, four black, king on queen, two pawns on king’s rook, three kings, bishop, two kings, bishop, three queen, five queen’s bishops, four queen’s rooks, four white continued, one pawn to knight, four rooks, pawn takes pawn, two pawn to queen’s rook.’
Quiz question: what was the exact date on which the game was played?
(3133)
The answer was given in C.N. 3154 (see page 277 of Chess, Facts and Fables).

White played 18 g3 mate. How did this conclusion occur in a game?
(3376)
Two clues: White gave the odds of his queen’s rook, and it was on b1 that Black lost his queen.
(3390)
The game in question is given below:
Andrés Clemente Vázquez – F. Paredes
Mexico, 1880
(Remove White’s queen’s rook.)
1 e4 e5 2 Nf3 Nc6 3 Bc4 Bc5 4 b4 Bxb4 5 c3 Ba5 6 O-O Qf6 7 d4 exd4 8 e5 Qg6 9 Ng5 Qxb1 10 Bxf7+ Kd8 11 Ne6+ Ke7 12 Ba3+ Kxf7 13 Ng5+ Kg6 14 Qxb1+ Kxg5 15 Bc1+ Kg4 16 Qe4+ Kh5 17 Qf5+ Kh4 18 g3 mate.
Source: Análisis del juego de ajedrez by A.C. Vázquez (Havana, 1889), page 122.
(3395)
On 7 February 2005 the UK television programme Mind Games (BBC Four) had William Hartston as a guest contestant. He was in fine form in the face of a thorny set of braintwisters. For instance, cuboid is a three-dimensional shape with six faces but also a word with six letters, and the teams were required to name another three-dimensional shape with the same number of faces as letters. It was Hartston who supplied the answer: dodecahedron (12 faces, 12 letters).
When he last did chess on television we do not know, but he is certainly the best presenter of the game we have seen.
C.D. Locock (1862-1946) described the following puzzle as the best he had made:
‘After 28 Ke8 Ke1 White mated on the move. One bystander observed that this was the tenth check in the game; and another that each side had eight undoubled passed pawns.’
Locock offered a prize to anyone who could construct such a game, but no correct solutions were received.
(3672)
For Locock’s solution, see C.N. 3708.
Some terse exchanges during a chess game:
White: ‘Helm knight.’
Black: ‘Kraal.’
White: ‘Munster.’
Black: ‘Minstrel.’
Umpire: ‘Machine.’
What does this mean?
(3772)
For the solution, see C.N. 3776.
In an impulsive burst of munificence we offer a book prize to the first reader who sends us the four-letter English word made up of the initials of the forenames and surnames of the two players pictured below. It is likely to mean defeat for many.


(3928)
The solution was given in C.N. 3942.
What is the correlation between the pieces and figures listed below?
King 9
Queen 5
Rook 8
Bishop 8
Knight 12.
(3950)
The answer is given in C.N. 3964.
From Jerry Slocum (Beverly Hills, CA, USA):
‘Sam Loyd did not invent the 15 Puzzle (or the 14-15 Puzzle) and had nothing to do with promoting or popularizing it. This is one of the surprising findings in a new book, The 15 Puzzle, which I have written with Dic Sonneveld. It describes and illustrates the true story of the invention, patent application and manufacturing of the puzzle.
A huge puzzle craze was created by the 15 Puzzle which began in January 1880 in the USA and in April in Europe. The craze ended by July 1880, and Sam Loyd’s first article about the puzzle was not published until 16 years later, in January 1896. Loyd first claimed in 1891 that he invented the puzzle, and he continued until his death a 20-year campaign to take false credit for the puzzle. Loyd also falsely claimed that he invented the game Parcheesi and a dexterity puzzle named “Pigs-in-Clover” that generated another puzzle craze in 1889.
The actual inventor of the 15 Puzzle was Noyes Palmer Chapman, the postmaster of Canastota, New York, and he applied for a patent in March 1880.’
Our correspondent’s book can be acquired direct from him on-line, inscribed if so wished.
(4406)
C.N.s 3389 and 3411 (see pages 305-306 of Chess Facts and Fables) discussed a letter to the editor on pages 124-126 of Lasker’s Chess Magazine, January 1905, which purported to contain reminiscences of Morphy under the pseudonym ‘Caissa’. At the conclusion of C.N. 3389 we observed that if all the personal statements in the article were correct, the writer (still alive in late 1904/early 1905) was born circa 1843, was already running a chess column in about 1858 and gave up chess some two years later.
We could, and can, think of no-one who fits the bill, but if the personal statements were not all correct Sam Loyd reverts to being a prime suspect. His track-record of dishonesty over his achievements is underscored by the fascinating book mentioned in C.N. 4406, The 15 Puzzle by Jerry Slocum and Dic Sonneveld (Beverly Hills, 2006). From page 75:
‘Sam Loyd has been correctly described as “America’s Greatest Puzzlist”, by Martin Gardner and many other writers. Although he deserves credit for his many wonderful puzzle inventions, he also had a reputation for using puzzles invented by Henry Dudeney, “England’s Greatest Puzzlist”, without crediting Dudeney, and taking credit for puzzles he did not invent. Loyd used his remarkable talent for making up stories about his puzzles to make his puzzles interesting as well as to spin tales about his accomplishments.’

Another example is on page 79:
‘Sam Loyd’s first puzzle column for the Brooklyn Daily Eagle was published on 22 March 1896 with a biography of himself. He began by claiming that “At nine years of age, he was champion of the New York Chess Club”.’
(4749)
Alan O’Brien (Mitcham, England) draws attention to two crosswords with a chess theme:
In both puzzles the clues are cryptic, in the British tradition for crosswords. To give just one (straightforward) example, the answer to the clue ‘Fireside game’ is ‘Poker’.
(4822)
Wanted: ingenious chess-related clues published in crossword puzzles. By way of example, below are three non-chess clues; the first two were reported on pages 100 and 101 of the Chambers Crossword Manual by Don Manley (Edinburgh, 2006), whereas the third one we recall from decades ago:
Country with its capital in Czechoslovakia (6)
HIJKLMNO (5)
(7)
(4853)
Steve Giddins (Rochester, England) recalls an old chess-related crossword clue, whereas the second specimen below is one we noted with a frown in puzzle 48 in Chipwinkle by Hubert Phillips (West Drayton, 1947):
Dramatic example of smothered mate (9)
As Ruy Lopez might have said: ‘From see to see’ (7, 4)
(4872)
For the solutions see the respective C.N. items.
Adam Ponting (Petersham, NSW, Australia) provides a link to a webpage concerning M. Mamikon’s ‘Mini-chess’, a puzzle which, it is stated, attracted the attention of Kasparov.
(8288)
On 11 April 2020 Olimpiu G. Urcan gave the puzzle on his Twitter page:
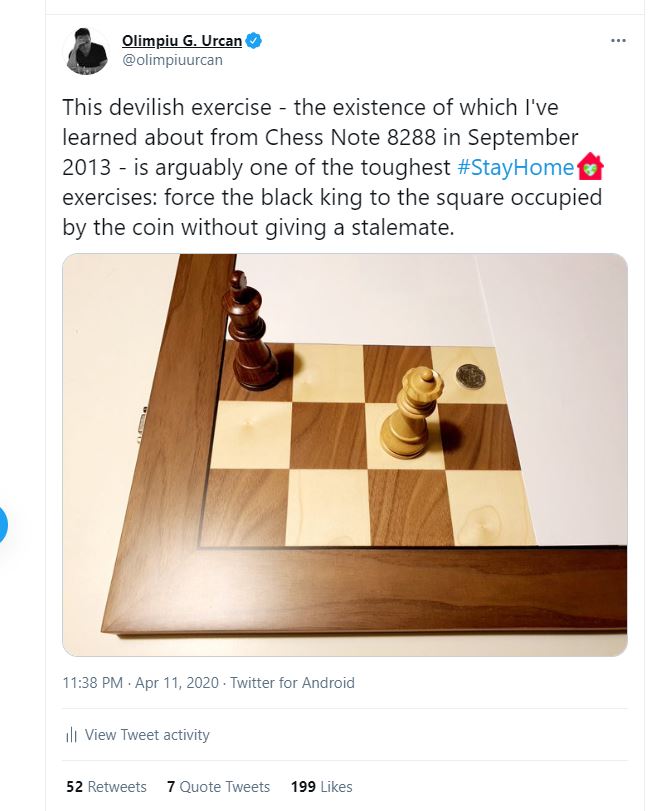

This is an extract from ‘How Puzzles Started’ by Sam Loyd, an article published on pages 41, 42 and 47 of Liberty, 12 March 1927.

The solutions will be shown in a future C.N. item. Loyd, it should be recalled, died in 1911.
The answers published in Liberty, 19 March 1927, pages 63-65:



The 32 units are placed on the board so that none can move.
(9278)
See C.N.s 9302 and 9356.
In a tournament a well-known player won a game against H.E. Atkins, who complimented him on his youthful verve. The player replied:
‘I am so grateful to you, but I do not feel youthful. The day before yesterday I was 51, and next year I shall be 54.’
Who was the player and where did his game against Atkins take place?
(10240)
‘I am so grateful to you, but I do not feel youthful. The day before yesterday I was 51, and next year I shall be 54.’
The speaker of these imaginary words was Amos Burn (born on 31 December 1848) after his game against H.E. Atkins in the Craigside tournament in Llandudno on 1 January 1901. (Page 543 of Richard Forster’s monograph on Burn notes that the game-score has not been found.)
There was a small anagrammatic clue with ‘I am so’, and the item was our adaptation of a puzzle (concerning Sherlock Holmes and Dr Watson, and with no chess connection) on page 47 of Murder at the Chessboard edited by ‘P.T. Houdunitz’ (New York, 2001).

Chess has only a few mentions in the book, whose title is derived from a simple detective story by Stan Smith on pages 116-119 concerning a game of monochromatic chess.
Another of the puzzles interspersed among the short stories has this unhelpful textless solution at the end of the book (page 239):

(10245)

On page 239 of Murder at the Chessboard edited by ‘P.T. Houdunitz’ (New York, 2001) the above was the (full) solution to a puzzle set on page 166.
Having placed a rook on one of the four centre squares of the board, Sherlock Holmes asked Dr Watson:
‘What is the minimum number of moves this rook needs to make in order to pass over all the squares on the board and then return to its original square?’
(10282)
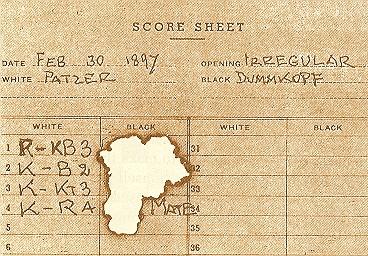
As mentioned in C.N. 4093, this score-sheet was given on pages 347-348 of The Colossal Book of Short Puzzles and Problems by Martin Gardner (New York, 2006), the task being to reconstruct the game.
Now we add, firstly, Leonard Barden’s chess column on page 13 of the Guardian, 24 December 1971:

The solution was on page 15 of the Guardian, 10 January 1972:

Leonard Barden, who has given us permission to show the two cuttings, does not recall his source for the puzzle, which was not his own invention. As mentioned in C.N. 4093, Randolph W. Banner, the contributor of the puzzle to Martin Gardner’s book, could say only that he ‘thinks he saw it in an English periodical published about 1920’.
Page 377 of The Complete Idiot’s Guide to Chess by Patrick Wolff (New York, 2005) ascribed the puzzle to Sam Loyd, but is that correct? The earliest publication that we can currently cite, with no composer stipulated, is page 53 of the Cincinnati Enquirer, 1 April 1934. However, see also pages 103 and 106 of Odesskie tayny Aleksandra Alekhina by Sergei Tkachenko (Moscow, 2016/17) and pages 89 and 92 of the 2018 English edition, Alekhine’s Odessa Secrets.
C.N. 4075 includes an adaptation that we concocted:

‘The Patzer, who moved only one
pawn, was so mortified by his quick defeat
that he burned the score-sheet. Did he burn it enough to
disguise how he was mated?’
(11372)

Which move has just been played?
(10802)
For the solution see C.N. 10805.

A Brief History of Puzzles by William Hartston (London, 2019) has much chess content, including not only such classics as Sam Loyd’s ‘Excelsior’ problem but also some unfamiliar specimens, of which a sample follows here.
‘What do the following have in common: the musicians Britney Spears, Eric Clapton, Roger Daltrey and Fats Waller; chess grandmasters Nigel Short and Tony Miles; actors Meg Ryan and Tom Cruise; politician Clare Short; TV personality Steve Irwin?
Hint: Aristotle could join them, and Socrates could do so twice.’
‘What do the words sine, ride, chess and chat have in common that is shared by riots, pest and zone, but not in the same place?’
‘I began [at an annual dinner of chessplayers at a London club] by presenting them with the letters A, B, C, D, E, F and asking them which letter was the odd one out.’
‘... Then I posed them a question that is definitely one of my favourites. It demands no chess knowledge [unlike the previous puzzle] and would, by most logicians at any rate, be considered fair:
Which of the following is the odd one out?
KING, king, king, king, queen’
Full solutions are given in the book.
(11617)
What is the connection between the game below and a world chess champion?

(11747)
For the solution, see C.N. 11759.
See too our feature article William Hartston.
Tailpiece (7 February 2021): Do not answer puzzles on-line in a way that spoils them for other people.
To the Chess Notes main page.
To the Archives for other feature articles.
Copyright: Edward Winter. All rights reserved.