Edward Winter
From page 33 of the Chess Weekly, 26 June 1909 (C.N. 5897)
Before turning to specific issues, this article offers a miscellany of our items about draws.
***
‘Regarding draws, I normally go along simply to play chess, without thinking beforehand in terms of a draw. Half-points suit me if I do not get the sort of game I want, or if these half-points enable me to attain a desired result in the event. In general one has to learn not to lose, and wins will then come of their own accord’.
Source: Anatoly Karpov: Chess is My Life by A. Karpov and A. Roshal (Oxford, 1980), page 59.
‘To the lover of beautiful chess, a draw is a very distasteful thing.’
Fred Reinfeld on page 123 of Great Moments in Chess, and quoted on page 109 of the April 1967 BCM.
(561)
In the 11th-round game between R.J. Broadbent and W.A. Fairhurst in the London tournament of 1946 the final position was:
White has just played 59 Kh3. Page 123 of the March 1946 CHESS, as well as page 59 of the tournament book, reported:
‘Broadbent v Fairhurst agreed a draw and the result was scored as such on the notice-board and (we believe) published as such in the papers. Some time afterwards Fairhurst found that in the final position he had a forced win and telephoned Broadbent to this effect, and, incredible as it may sound, the two agreed to ask the Committee to amend the result to a win for Fairhurst. Still more fantastic, the Committee accepted the amendment!
With the best will in the world we cannot find anywhere in the rules any justification for the alteration of the legal result of a properly-conducted game (the result in this case being, of course, a draw by agreement) by any subsequent process, and therefore we score the game as a draw.’
(2479)
Our footnote on page 46 of A Chess Omnibus:
This incident was subsequently discussed in a brief article by Alistair Maxwell on page 12 of the October 2002 Scottish Chess. On the basis of a Fairhurst notebook, the concluding moves were given as 59...Bf4 60 Qg4 Be5 61 h5 c6 62 Qg2 Qe3+ 63 Kh4 Qxd3 and wins.
‘He has probably conceded more drawn games when having a positional advantage than any other chessplayer.’
Source: BCM obituary of the appropriately-named J.A.J. Drewitt (April 1931 issue, pages 166-167). The obituary also reported that ‘he was a brilliant conversationalist on the very rare occasions when he could be persuaded to talk’.
The above item was given on page 387 of Kings, Commoners and Knaves.
A position taken from page 42 of Chess Potpourri by Alfred C. Klahre (Middletown, 1931):
White draws, whether or not he has the move.
The composition is by Eugene B. Cook (1830-1915), who, shortly before his death, sent it to Alain C. White with this comment:
‘The king and peasant quietly enjoy their hermitage, while two complete armies of the black heathen rage without.’
(3103)
The problem was first published by Alain C. White on page 67 of the April 1915 American Chess Bulletin, at the end of a three-page appreciation of Cook.
Concerning remarks such as ‘All rook endgames are drawn’ see our feature article so titled.
Page 3 of the Chess Player booklet Emil Schallopp (Nottingham, 2008) lists the master’s main tournament and match results (1864-1907). The totals are +163 –170 =38, and page 2 comments that ‘one extraordinary feature of Schallopp’s play is his small number of draws in major events’.
Emil Schallopp
(6001)
‘A draw can be obtained not only by repeating three moves, but also by one weak move.’
Wanted: further particulars about this remark. It was ascribed to Tartakower on, for instance, page 28 of Secrets of Chess Training by Mark Dvoretsky (London, 1991).
(6781)
C.N. 888 quoted from page 7 of CHESS, 14 September 1935 a remark by Alekhine:
‘It is practically impossible nowadays to force a winning position with the black pieces against a player of master strength (even if not absolutely first-class standard) who is content to play for a draw.’
(7178)
William Hartston’s new book The Things That Nobody Knows (C.N. 7280) has one item about chess, which we reproduce from pages 166-167 with the author’s permission:
‘What is the result of a chess game if both sides play perfectly?
With best play, the game of noughts-and-crosses (tic-tac-toe in the USA) should end in a draw, as it is not difficult to demonstrate. In the more complex game of Connect Four, it was shown by exhaustive analysis in 1974 that the first player can force a win. The still more challenging game of gomoku (five in a row) was solved by computer in 1994, showing that the first player may again force a win with best play. But what about chess?
Results from international tournaments have supported the general view that White, who moves first, has an advantage, with results for White around 2 or 3 per cent ahead of Black. With around 10120 possible chess games (which is significantly more than the number of atoms in the universe, estimated at around 1080), a complete analysis of chess is currently impossible. Whether White’s advantage is enough to win, or whether Black can defend himself, or whether indeed with best play Black should actually win, at present appear to be unfathomable questions.’
It is certainly a widely discussed issue. Two passages from nineteenth-century books may be mentioned here, the first being on page xxxi of The Modern Chess Instructor by W. Steinitz (New York, 1889):
‘In fact it is now conceded by all experts that by proper play on both sides the legitimate issue of a game ought to be a draw, and that the right of making the first move might secure that issue, but is not worth the value of a pawn.’
From pages 74-75 of Maxims and Hints by R. Penn (London, 1842):
‘Every game perfectly played throughout on both sides would be by its nature drawn. Since, then, in matches between the most celebrated players and clubs of the day some of the games have been won and lost, it seems to follow that there might be better players than have been hitherto known to exist.’
We recall too the article ‘Quelques réflexions sur la partie idéale’ by L. Roussy which was published, together with comments by Erwin Voellmy, on pages 54-58 of the April 1919 Schweizerische Schachzeitung/Revue suisse d’échecs:
The article also appeared on pages 134-137 of the June 1919 La Stratégie. Page 299 of the September 1919 BCM noted Roussy’s conclusion that White wins a perfectly played game but remarked that ‘M. Roussy does not go so far as to produce an example of a game perfectly played by both sides, in which the victory goes to White’. A book prize was offered by the BCM to ‘the reader who shall be adjudged to have sent in the nearest approach to “perfection”’.
B. Goulding Brown expressed doubts about Roussy’s thesis in a letter on pages 334-335 of the October 1919 BCM but added:
‘... undoubtedly the advantage of first move, added to that gained from one slightly objectionable move on Black’s part, will produce a winning advantage for White, as in the game H.E. Atkins v J.F. Barry (Cable Match, 1910), which I beg to enclose as the nearest that I know to perfection.’
Regarding that game, see pages 142-143 of A Chess Omnibus
(C.N. 2229).
(7306)
On the subject of the New York, 1889 tournament, John Blackstone (Las Vegas, NV, USA) points out this item on page 14 of the New York Sun, 26 May 1889:
‘The two drawn games which Messrs. Weiss and Chigorin performed, we will not say played, on Thursday and Friday of last week, while in the effort to break their tie for first place, added no glory to the history of chess. Under such deliberate attempts at a draw, chess is put behind the game that ranks next to it, checkers, in which drawn games are the rule and not the exception. The pusillanimous resignation to rivalry with which each of these two leaders of a great intellectual diversion shrank from the attack, hoping that his adversary would make a mistake, is but another phase of the famous meeting in Canada between Mace and Coburn. Those eminent prize-fighters quartered about the ring for hours because neither was willing to lead for the other, and the affair ended in the same sort of fiasco as these concluding encounters of the chess tournament.
Masters Chigorin and Weiss should gird up their loins and be men when they meet tomorrow. Let them abandon their imitation of Mace and Coburn and think of how Chateaubriand used to say, in a language they both can read, “Ce n’est pas la victoire [qui] fait le bonheur des nobles coeurs – c’est le combat.” [This quote is commonly ascribed to Montalembert, with la joie rather than le bonheur.] Not victory, but battle, delights the noble heart. One blow for the honor of chess rather than none for victory. Play for all you are worth.’
Notwithstanding the newspaper’s exhortations, the fourth and final game in the play-off was drawn in 28 moves the next day.
(7835)
Steinitz writing on page 267 of the September 1887 International Chess Magazine:
‘To my mind it is clear from long experience that the greatest evil that has to be contended with in tournaments is the scoring of the draws absolutely, and the system of the London tournament of 1883 is by far the best compromise that can be effected in order to make tournaments a real test of superiority.’
(8007)
‘It is an axiom in chess that he who plays to win a drawn game loses it.’
Source: Chess Player’s Magazine, 1 August 1867, page 229.
(8425)
The front cover of Caïssa, 1 May 1950 has been forwarded by Alan McGowan (Waterloo, Canada):
The magazine gave no explanation (concerning the context, for instance, or the rotation of the chessboard), but Mr McGowan notes that, as mentioned on page 129 of the issue, the Candidates’ tournament in Budapest was in progress. One of the games between Bronstein and Kotov was drawn in 15 moves.
(8437)
Charles Milton Ling (Vienna) asks whether a reliable source is available in support of his recollection that the phrase ‘Genug des Stumpfsinns, Remis!’ (‘Enough tedium, draw!’) has been attributed to Richard Teichmann, who wished to attend a wrestling event rather than play chess.
We can offer a passage about Teichmann from page 58 of Ein Rundflug durch die Schachwelt by Rudolf Spielmann (Berlin and Leipzig, 1929):
‘In einer Wettkampfpartie mit Sämisch begab sich folgendes: Etwa 15 Züge waren geschehen. Sämisch glaubte nach allen Regeln moderner Schachkunst eine aussichtsreiche Stellung erlangt zu haben und war eben eifrig dabei, einen geeigneten Schlachtplan auszuhecken. Während er angestrengt nachdenkt, zieht plötzlich Teichmann die Uhr, steht auf, schiebt die Steine zusammen und bemerkt einfach: “Genug des Stumpfsinns, Remis!” Empfiehlt sich und geht in den Zirkus. Er war höchste Zeit, denn die Ringkämpfe hatten eben begonnen!’
Is it possible to find a match-game between Teichmann and Sämisch which fits this account (i.e. after about 15 moves Sämisch had an apparent advantage, but Teichmann suddenly broken off the game as a draw since he wished to watch wrestling at the circus)?
Page 43 of the February 1922 Deutsche Schachzeitung reported that a brief match between the two masters had taken place in Berlin. Teichmann won with one victory and three draws.
(8449)
Concerning the remark ‘Genug des Stumpfsinns, Remis!’ (‘Enough tedium, draw!’) attributed to Richard Teichmann, Birger Flindtholt (Randers, Denmark) has found the following (Caïssa, January 1952, page 29):
(8836)
‘He [Schlechter] was widely known throughout his career as a drawing master, usually content to split the point even with much weaker players, but very difficult to beat.’
Source: The World Chess Championship A History by Al Horowitz (New York, 1973), page 63. (Almost identical sentiments appeared in Horowitz’s column in the New York Times, 5 March 1972, page D 31.)
‘The designation “drawing master” for Carl Schlechter can be taken with a grain of salt.’
Source: Solitaire Chess by Al Horowitz (New York, 1962), page 69. (The item originally appeared on page 209 of the July 1960 Chess Review.)
(8506)
A remark by Cecil Purdy on page 16 of the Australasian Chess Review, 25 January 1939:
‘It is usually no harder to win a drawish game than a losish game, and the latter has the disadvantage that you may lose.’
(9225)
C.N. 9480 discussed ‘the most beautiful tournament draw’ (Halprin v Pillsbury, Munich, 1900).
Concerning this study by William Edward Rudolph, see A Chess Fortress.
See too Stalemate, Repetition of Position or Moves in Chess and Chess: the 50-move Rule.
Robert John McCrary (Columbia, SC, USA) writes:
‘I have a candidate for the origin of the term “draw” in chess. It is found in The Famous Game of Chesse-Play by Arthur Saul (1614), in Chapter III on roughly page B3 or B4 (numbering unclear), under the heading “A Caveate for such as will condition to give a Mate”, and reads as follows:
“Imagine that two were a playing, and that many men on both sides were lost and no odes in the men of either side, so that the game were indifferent, that then I say, one of the gamsters should give over the game and draw his stake, the other at this seeming to be a-grieved, thinking his men standeth better then the others which hath given over, he saith, had you playd out the game I should have wonne it, & the other replying, demandeth what hee will lay more one the game, the party a-grieved upon this offereth a crowne more, that hee will winne the Mate, now here is a condition, which if hee performe not he looseth both his first and last stake: The way for him that taketh any man upon such condition, is still to change, and to bring it unto a dead game, and so shall he this way winne the stakes, by reason the other had tyed himselfe by obligation to give the Mate, wherefore let any one take heed how he entreth into such condition; for who so doth it giveth the other advantage, whether it be at the beginning of the mate, or after, it is all one.”
My theory that the Saul text may be the origin of the term “draw” in chess is based on two considerations: 1) it refers to an “indifferent” game, in which many men have been lost, i.e. evidently one without winning prospects; 2) according to the Oxford English Dictionary (definition number 37) the term “draw the stakes” referred at that time (before 1614) to a situation in sport in which one (with)drew either the stakes or an entry (such as a horse) from the competition. I suggest that by 1614 chessplayers were modifying that sporting meaning slightly to allow a player to “draw the stakes” (i.e. withdraw them) if a game in progress reached a simple endgame that clearly could not be won, as Saul describes.
In 1640 Joseph Barbier published a revised edition of Saul’s book. It was, in fact, a substantial rewrite which contained at least as much Barbier as it did Saul. Barbier omitted the passage from Saul referring to “draw the stakes”, but included a point with similar meaning in his proposed code of laws, in which he used the term “dead game” but not the word “draw”. At one point, Barbier defined “dead game” as a king versus king ending, but within a context that would apply just as well to any simplified, drawn ending. Since “dead game” was also used by Saul in his passage, I believe that Barbier’s terminology tends to support the idea that Saul’s use of “draw the stakes” in a passage that also referred to “dead game” was, in fact, a new application of the sporting term “draw the stakes” to drawn endgames in chess, and thus possibly the origin of our term “draw”.
The earliest use that I have found of “draw” with the modern meaning is in Richard Lambe’s The History of Chess (1764). It uses “drawn game” on pages 119, 123 and 127 and “drawn” on page 120. These antedate the OED reference for “draw” in chess (definition number 38). The three references in Lambe’s book use only the phrase “drawn game”. The first is just the words “drawn game” (no sentence) at the end of analysis of the “Queen’s Gambit, or Gambit of Aleppo”. The second (page 123) ends another game analysis with the note “It must be a drawn game, because to win the B.P. you must lose your R”.’
(4666)
Robert John McCrary adds:
‘In C.N. 4666 I set out my theory that the word “draw” comes from a rule expressed in 1614 in Arthur Saul’s The Famous Game of Chesse-Play. That rule, given verbatim in C.N. 4666, states that a player may “draw stakes” (withdraw from the game) in an “indifferent” game with few men left and no winning prospects. To avoid abuse of this practice, the opponent could increase the stakes and guarantee to win.
I have now found the same theory in another sport. Pages 57-58 of The Dictionary of Cricket by Michael Rundell (Oxford, 1995) have the following in the entry for “Draw”:
“In fact, the word ‘draw’ itself, in its sporting sense, derives from the practice of ‘drawing’ or ‘withdrawing’ the bets made on a contest when its issue was undecided.”
The book gives three examples of this use (“drawn battle”, “they drew stakes” and “London drew with Dartford”) from periodicals’ reports on undecided cricket matches in the 1730s.’
(8341)
Below is the entry for ‘Remismonde’ on page 171 of Dictionary of Modern Chess by Byrne J. Horton (New York, 1959). Any information confirming, refuting or complementing the entry will be gratefully received.
‘A term coined by Dr Tarrasch (1862-1934) which he applied to [Carl] Schlechter of Vienna. Schlechter was known to have terminated many of his games as drawn games. Hence, Dr Tarrasch referred to him as the “Master of the Vienna Remismonde”.
Literally, “Remismonde” is a compound French word. Remis in chess terminology means a draw. (See Dictionnaire de la Langue Française, by E. Littré, Paris, 1883.) Monde means world. There is no completely satisfactory or precise explanation of this compounded word. Dr Felix Pollak of Northwestern University, a passionate chessplayer from Vienna, offered the following explanation. He wrote: “I believe it is simply a play on words, coining a parallel expression to ‘demi-monde’ (denoting a lady of the ‘half-world’ i.e. of easy virtue). Hence, calling Schlechter the Master of the Remismonde denotes Schlechter to be king of the drawing world, the Master of the Vienna ‘Grand-Master-Drawers’.” Mr Hans Kmoch, the renowned Secretary and Manager of the famous Manhattan Chess Club, concurs with this explanation.’
(4367)
Siegbert Tarrasch
C.N. 4367 asked for information about a term ascribed to Tarrasch, ‘Remismonde’, and we now note the following on page 63 of the August 1898 American Chess Magazine:
‘Personally, he [Tarrasch] is a gentleman of the world, with the most elegant of manners; genial, sarcastic, witty and sharp-tongued. “Ah!”, he exclaimed once, when the dear Viennese again brought about a “draw”. “I am here in Vienna among the ‘Remismonde’.” “It is not sufficient to be a good chessplayer, one must play good chess”, is one of his favorite sayings.’
The writer was Armin Friedmann in Pester Lloyd, 20 or 21 June 1898. The original German version was given on page 346 of the Vienna, 1898 tournament book:
‘Persönlich ist Dr Tarrasch ein Weltmann von feinsten Manieren, geistreich, boshaft, witzig, scharfzüngig. “Ach ich verkehre hier nur mit der Remismonde”, seufzte er jüngst, als die lieben Wiener nach ihrer Gewohnheit sich wieder einmal ausglichen. “Es ist nicht genug, dass man ein guter Spieler ist, man muss auch gut spielen”, lautet einer seiner Aussprüche.’
Spoof variants on the ‘good chessplayer’ dictum were discussed on pages 396-397 of Kings, Commoners and Knaves, but what earlier citations can be found for Tarrasch’s own words?
(4868)
A.R.B. Thomas came up with the following proposal on page 118 of CHESS, 24 January 1960:
‘I suggest that players in a tournament should be allowed to agree that one take three-quarters of a point and his opponent a quarter. A player is often disinclined to accept a draw but not certain that he can win; the three-quarters of a point might satisfy him and a safe quarter-point might be acceptable to his opponent. Such a result could be quite helpful to an organizer pairing up in a Swiss tournament.’
(3036)
Robert John McCrary writes:
‘When did the system of counting draws as a half-point start? On page 8 of Transactions of the British Chess Association, 1866-67 I have found the following passage in the report on the preliminary meeting (3 September 1867) regarding that month’s tournament in Dundee:
“The Grand Tournament comprised ten competitors, each of whom was to contend one game with every other combatant, the prizes to be awarded according to the scores thus made. In order to obviate the difficulty experienced at the recent tournament in Paris, it was decided that a ‘draw’ should be reckoned as half a game to each player engaged in it.”
The tournament results on pages 8-9 gave the scores with the half-points included.
It is difficult to use modern compilations to determine when the “half-point” system began, because modern compilers sometimes present tournament and match scores of that period with the half-points even if the original tables did not use the system. So, which other original sources help to pinpoint the beginning of the half-point system for draws?’
(5605)
Kristo Miettinen (Rochester, NY, USA) asks about the various ways in which draws have been scored in chess tournaments and matches since the mid-nineteenth century:
‘For instance, the phrase “draws do not count” in match play has meant different things at different times; in the first American Chess Congress, at New York in 1857 (to name but one early event) drawn games did not count even for purposes of alternating colors, so that two players who drew played their next game with the same colors as in the draw, until a decisive result was scored. Only after decisive results were colors alternated.
Many descriptions of nineteenth-century tournaments also mention that drawn games had to be replayed, but without indicating whether colors were alternated for the replay.
Other oddities include the Paris, 1900 tournament, in which draws were replayed once only, with alternation of colors, but a second draw stood as the final result.
My interest is in the effect that such rules may have had on opening selection. For instance, rules that required a player with the black pieces to continue playing black until he won (or lost) a game would strongly discourage playing to draw from the outset with Black, regardless of the opponent.’
Do readers know of any systematic treatment of this matter?
It will be recalled that some tournaments deviated from the practice of awarding half a point for a draw. A notable example was Monte Carlo, 1901, and we quote from page 373 of the December 1900 issue of La Stratégie:
‘La première partie nulle comptera pour ¼ à chaque joueur et devra être rejouée; si l’un d’eux gagne la seconde elle lui sera comptée ¾ en tout; si elle est encore nulle chacun aura ½ point. Cette modification pour les nullités a été suggérée par M. le Dr E. Lasker.’
Or, as Jeremy Gaige summarized the system on page 171 of volume two of Chess Tournament Crosstables (Philadelphia, 1971):
‘Initial games, if drawn, counted ¼ and were replayed. If the replayed game was drawn, both players won another ¼. The winner of a replayed game received ½, the loser 0.’
The identical wording turned up on page 6 of Chess Results, 1901-1920 by Gino Di Felice (Jefferson, 2006).
In case of a draw at Monte Carlo, 1901 there was alternation of colours for the second game. See, for instance, A.J. Gillam’s booklet on the tournament (Nottingham, 1995) and, in particular, the discussion of the experimental scoring system on pages 67-70.
(6671)
From Robert John McCrary:
‘In early events the English rule was that a player retained the first move for the next game when a game had been drawn. This did not necessarily mean keeping the same color, as the rule that White moves first was not fully established until later.
That rule was in effect for the McDonnell-Labourdonnais games, because it was “according to the English law” (page 374 of the fourth volume of the Chess Player’s Chronicle, 1843). Staunton’s The Chess-Player’s Handbook (London, 1847) stated on page 36 that players alternate the first move, except that “If a game be drawn, the player who began it has the first move or [sic] the following one”. This is presumably why the First American Chess Congress (New York, 1857) used this rule, as page 63 of that tournament book stated that the Code in Staunton’s Handbook would govern play, adding on page 64, “Drawn games are not to be counted”.
However, a movement to change this rule was evident as early as 1844. Page 156 of that year’s Chess Player’s Chronicle (volume five) noted that the match between Stanley and Schulten in New York required the first move to alternate even in case of draws. On pages 252-253 of that same volume a correspondent advocated requiring that the first move alternate even in case of draws. Staunton expressed agreement with that change, which he said was already the rule in France and, he believed, throughout the continent. Thus, it seems that Staunton’s publication of the old rule in his Handbook was based on earlier codes, and not necessarily on his own opinion.
On page 188 of the London, 1851 tournament book Staunton said that the players at that event had voted to alternate the first move even in case of draws, although this rule had been forgotten or ignored in one of the games.’
(6676)
In a letter on page 441 of CHESS, 20 August 1955 P.N. Wallis of Quorn referred to ‘dull and unenterprising chess which is prevalent in this country’, adding:
‘The remedy is quite simple. In the British Championship and similar tournaments let a win count 3 points and a draw one to each player, thus putting a premium on the win.’
On page 454 of the 30 September 1955 issue, R.W. Ives of Leeds responded:
‘Mr Wallis raises an old issue. James Mason in 1895 advocated allowances of 1, 0 and minus a half for a win, a draw and a loss respectively, and this seems to me mathematically more logical than the present system. Certainly it seems now that quite a few halves can be picked up in a congress without much thinking. Why should a pre-arranged draw improve either player’s score? The position should be the same as before they started. A player who has lost has a worse record after the game than when it started. Can your readers work it out?’
Writing from Belfast, A.S. Russell commented in CHESS, 15 October 1955:
‘Mr P.N. Wallis proposes that a draw should count only one-third as much as a win. This is intended to penalize the player who adopts stodgy drawing variations. To me it seems that it might have the opposite effect.
Suppose an enterprising player meets a draw-minded opponent, he is faced with a difficult problem. If he ventures on risky play to avoid a draw ... he runs great danger of losing and handing an easy three points to the very type of player Mr Wallis wants to penalize.
The solid player would not now plod along half-way down the table but would bound ahead, aided by bonus points gained against desperate opponents risking too much to avoid the penalizing draw.’
A contribution from C.J.S. Purdy of Sydney was published on page 93 of the 10 December 1955 issue:
‘R.W. Ives (CHESS, 30 September) did not realize that James Mason’s proposal to award 1,0 and minus a half for a win, draw and loss respectively is mathematically exactly the same as P.N. Wallis’s proposal to count a draw as worth one third of a win. This is easily seen if you add a half to every player’s score in every game, irrespective of his result (this cannot affect the positions). You then get 1½, ½, 0; or, eliminating fractions, 3, 1, 0, which is Mr Wallis’s system. Less drastic, of course, would be 5, 2, 0. Mathematically, there is no objection whatever to penalizing draws.
In CHESS of 15 October, A.S. Russell raises an objection which is much less weighty than many players imagine. His objection is that by deliberately playing “stodgy drawing variations” players can induce strong opponents to play wildly and thus lose. The old bogey that it is a great handicap to meet an opponent who plays deliberately for a draw, and that one has to play mad gambits to circumvent him, dies hard. Botvinnik, when three points up against Smyslov, could have won the match easily had there been anything in this theory. It “cuts both ways”. The draw-monger will fail to make the most of his position, and thus give his opponent chances to gain ground, e.g. Capablanca against Lasker at St Petersburg, 1914, where Capablanca played “drawishly” instead of seeking to exploit his two bishops aggressively, and lost. I see no objection to one player trying to draw – only to both players trying to draw. Penalizing draws would certainly eliminate that. Admittedly, many draws are genuine, and it is a drawback that all would be equally penalized. But not as great an evil as arranged draws, which give some players extra rest days. These draws are not merely “drab”. They are cheating.’
W. Heidenfeld of Johannesburg replied on pages 153-154 of CHESS, 11 February 1956:
‘In your “drab draws” correspondence C.J.S. Purdy writes: “Admittedly, many draws are genuine, and it is a drawback that all would be equally penalized. But not as great an evil as arranged draws, which give some players extra rest days.” It is hard to believe that your correspondent is serious in his suggestion that draws of whatever nature should be “penalized”, seeing that chess – like cricket – is a game that allows for a very wide drawing margin; a game that regards players as equal who are merely “approximately equal” and that does not insist that differences of split seconds or fractions of inches in performance are to be rewarded by plus and minus signs. In athletics “draws” are few and far between; in tennis they do not exist at all; and it would have been simple enough to have chess decided on similar lines.
It is clearly illogical not to object to one player trying to draw, but to object to both players trying to draw – if the draw serves the purpose of both. Playing in a tournament, your object is not to win the game – any game – but to win the tournament; and where playing for a win at all cost does not conform to this aim, even the temptation to do so must be firmly resisted. In fact, the ability to resist this temptation is part of a successful player’s technique. Some of the most glorious strokes of cricket may have to remain unplayed – some of the most imaginative games of chess to remain unconceived – because the player has the will to win ... the match or the tournament. In other words, it is exactly the will to win that may dictate to you the necessity of drawing an individual game. Players who do not possess this will to win may indulge their fancy at leisure – but they hardly deserve to get an extra bonus for it.
Leaving aside the special case of the “drab” draw, I believe that masters and annotators have a lot to answer for the [sic] general contempt of “drawn games”. It does not suit their book to annotate such games – because obviously it is far more difficult to assess a good fighting draw correctly than it is to come to definite conclusions regarding the merits of a won and lost game. In the latter, the fact that one side lost is in itself a clear indication of some inferior moves somewhere or another. But in a drawn game – did White stand to win? Did Black? Or was what Lasker called the Remisbreite never exceeded all through the game?
Looking at draws without passion or emotion, one must surely realize that they are the best chess games of all. The best draws must be better games than the best wins – neither side made a mistake sufficiently serious to enable the other, even with best play, to swing the balance in his favour. Yet how many anthologies of famous games have such draws? Games like Alekhine v Réti, Vienna, 1922 or Alekhine v Marshall, New York, 1924? At best very short games of this nature, like the famous draw between Pillsbury and Halprin at Munich, 1900, or the equally famous first encounter between Botvinnik and Alekhine at Nottingham, 1936, are “tolerated”.
If, in such games, the defender had been a little less alert, had lost his way, no matter how slightly, just once, they would rank among the very best specimens of fighting chess. And because the defence was perfect they don’t? Is this the famed chess players’ logic?
I am at present working on the MS of a book “Battle in the balance”, a collection of the finest draws of modern chess, from Hamppe v Meitner, 1872 to Schmid v Castaldi, Venice, 1953. During these 80 years some 50 to 60 practically perfect games of chess were played –and the great majority of them are almost completely unknown.’
The references above to James Mason’s proposal in 1895 concern the extensive correspondence (also involving E.N. Frankenstein and W. Sonneborn) published in the BCM that year and in 1896. However, Mason had made his proposal in a letter (London, 10 December 1892) on pages 40-43 of the January 1893 BCM. On page 42 he wrote:
‘A win should count 1, a draw 0, and a loss minus ½ only, it being in reality no more. It takes two to make a game. What any player loses in losing any particular game is not the whole of that game, but only his own individual half of it, or his chance of winning it. The game counts 1 to the winner; that 1 is made up of twice ½ – his own ½ and his opponent’s ½ – only one of which is, strictly speaking, either won or lost. In fine, the system here proposed is a natural system, and the only one which can be substituted for the present system with advantage to all concerned. It would encourage every player in a tournament to do his best to win, the draw being valueless for scoring purposes.’
(10251)
Regarding Draw! by Wolfgang Heidenfeld, C.N. 394 (see page 234 of Chess Explorations) gave a selection of quotations:
A brief selection of quotes from Draw! (London, 1982) should serve as a reminder of Heidenfeld’s outstanding writing skills:
(After a sober analysis of Hamppe-Meitner, Vienna, 1872): ‘The treatment of this game in chess literature suggests how easy it is to be dazzled by its ingenuity, captivated by its charm, until one’s critical faculties are suspended and one believes everything one sees.’ (page 5)
(On the short draw Alekhine-Botvinnik, Nottingham, 1936): ‘On the whole, a grossly overrated game.’ (page 6)
‘Pillsbury, generally regarded as a great attacking master, was really the first player to plan his attacks with an eye to the end-game – his games often show profound combinations, not for mating purposes but in order to obtain an advantageous ending.’ (page 14)
(On Charousek and Fähndrich v Halprin and Marco, Vienna, 1897): ‘The most thrilling Muzio Gambit ever played.’ (page 17)
(After a quote from the Munich, 1900 tournament book): ‘I quote this passage with particular pleasure, not only for the sentiments expressed, but also in order to acquaint present-day players with the racy diction of the inimitable Georg Marco. It may give them an idea of how much they lose by notes in the ever-encroaching Informator style, through which the greatest entertainment ever invented is reduced to a series of mathematical symbols.’ (page 21)
(On the seventh match-game, Schlechter-Lasker, Berlin, 1910): ‘It is probably the most profound game ever played in a world championship match.’ At the end of his (wonderful) annotations to the game Heidenfeld concludes: ‘And yet there are people who maintain that Karpov and Korchnoi are stronger than Lasker and Schlechter. They must be joking.’ (pages 26 and 30)
(Tarrasch): ‘In the years after the first war to end all wars he played games of a charm and a depth inconceivable perhaps to the disciplinarian of earlier years . . . One does not always perform best when driven by a mission.’ (page 36)
‘Reuben Fine is probably the most underrated player in the history of the game . . . Both his sporting results in the thirties and the sheer quality of his games make him one of the outstanding players – possibly the outstanding player – of the period.’ (page 97)
(394)
The first two paragraphs of his Introduction (page 1):
‘Drawn games have a poor press. Far too often the result is reached without a fight: the players do not want to play chess but score half a point.
And yet who can doubt that draws that are both well-fought and free from major error (though chess is so complicated a game that what Suetin calls secondary errors are virtually unavoidable in a real fighting game) constitute the highest form of chess? Where every brilliant attack finds an equally brilliant parry, where each “unexpected” combination is in fact expected and therefore met successfully, we have no victor and no vanquished. But even such nearly flawless games are often little-known merely because they carry the mark of Cain of the unshed blood.’
Few masters have had their birth announced in a chess magazine, but here is a case that comes to mind:
‘Mr Heidenfeld, now living in Dublin, has just been presented by his wife with a son, Mark. World champion, 1998?’
Source: CHESS, 13 June 1968, page 292.
Wolfgang Heidenfeld was a fine, incisive chess writer, and below is an excerpt from a letter he wrote us from Dublin on 22 March 1978:
‘Not only am I at present collaborating with Tim Harding on an opening book for the Batsford series (my first ever, since I hate books on the openings!), but after that I may have, literarily speaking, the chance of a lifetime: the possibility of bringing out a greatly improved and enlarged version and translation of Grosse Remispartien (under the far more attractive title “Battle in the Balance”). This I have always regarded as my magnum opus – spoilt to a large extent by the skimpiness of the publishers (it is the ONLY book I have ever seen in which even the dedication is squeezed onto the first page of text!!). The matter is not 100% yet – but if it comes off, every other chess project is automatically out. The new version would require at least six months’ concentrated work.’
The English edition of Grosse Remispartien was eventually published, under the title Draw!, in 1982, the year after Wolfgang Heidenfeld’s death. Edited by John Nunn, it was of outstanding quality.
(2733)
When the above item was reproduced on page 203 of A Chess Omnibus we added this footnote:
The book on draws was a long-term project of Heidenfeld’s. On page 154 of CHESS, 11 February 1956 he wrote: ‘I am at present working on the MS of a book, “Battle in the balance”, a collection of the finest draws of modern chess, from Hamppe-Meitner, 1872 to Schmid-Castaldi, Venice 1953.’
The mistakes in players’ names and game venues in Draw! by Leonid Verkhovsky (Milford, 2014) are so numerous and obvious that we do not intend to list examples unless challenged to do so. The imprint page states, ‘Editing and proofreading by Peter Kurzdorger’. A former Editor of Chess Life is Peter Kurzdorfer.
(9098)
Siegrun Macgilchrist (Maybole, Scotland) asks for biographical information on Leonid Verkhovsky. Can readers suggest any particularly good sources?
Verkhovsky is best known for his 1972 book Nichya!; a Spanish translation, Tablas, was published the following year. A second Russian-language edition appeared in 1979; regarding the shoddy English version (Milford, 2014) see C.N. 9098.
Verkhovsky also wrote a book on Zugzwang (Moscow, 1989), and an Italian translation came out in 1992. Another work is a monograph on Schlechter (Moscow, 1984), with a Foreword by Lev Polugayevsky.
(10640)
Vitaliy Yurchenko (Uhta, Russian Federation) notes the information about Verkhovsky on the back cover of a 2005 book by him:
Dan Scoones (Port Coquitlam, BC, Canada) draws attention to a webpage about Evgeny Gik with references to Verkhovsky having died and another Russian page featuring a photograph of Verkhovsky with Vladimir Lepeshkin.
(10643)
Wanted: drawn games which were awarded a brilliancy prize. The best-known case is probably Geller v Golombek, Budapest 1952, if only because Black has so often written about it. An earlier example was Mieses v Pillsbury, Vienna Gambit Tournament 1903. Mieses annotated the game on pages 148-150 of the May 1941 BCM, this being his final note:
‘This game was awarded a brilliancy prize with both players sharing it, since the adjudicating Committee expressed the opinion that the ingenuity of the attack, on the one side, and the skill and doggedness of the defence, on the other side, deserved the highest praise. A draw winning a brilliancy prize is quite unique in the history of tournaments.’
(1547)
From Ed Tassinari (Scarsdale, NY, USA):
‘A drawn brilliancy that immediately comes to mind is Medina v Torán, Palma de Mallorca, 1968, which is annotated on pages 171-172 of Heidenfeld’s Draw!’
We add that Heidenfeld’s book (page 138) draws attention to another case, Heidenfeld v Pachman, Madrid, 1960. The chairman of the committee appointed to award the special prizes, Roman Torán, had stated, ‘A draw has no claim to being considered at all for such an award’, but Heidenfeld counters with three arguments:
a) There was the Vienna 1903 precedent; b) The game chosen at Madrid for the prize ‘was later found to contain a hole as big as a house (in the winner’s play ...)’; c) Torán himself subsequently won such a prize. ‘It is not known that he refused to accept the award on the grounds that a drawn game should not be eligible.’
(1575)
Michael Furmston (Shipham, England) adds Rossolimo v Nestler, Venice, 1950 (see pages 39-40 of the November 1950 CHESS).
(1621)
On page 232 of the August 1970 BCM Wolfgang Heidenfeld wrote:
‘... a phrase like “Alekhine’s Best Games” is really ambiguous: it may mean two entirely different things, viz. (a) the games Alekhine played best and (b) the objectively best games in which Alekhine was a participant (in which the standard of the game is achieved by both partners) – thus he need not necessarily have won them. This, in fact, is the basis of my anthology Grosse Remispartien.
In fact, it is little short of ludicrous that Alekhine’s Best Games does not contain his draw against Marshall at New York, 1924, where a most original and new strategic conception by Marshall is met by an amazing tactical finesse of Alekhine’s, the whole (drawn) game being one of the greatest ever played. It is similarly ludicrous that Golombek’s anthology of Réti’s Best Games is without his draw against Alekhine at Vienna, 1922 – which has been christened the Immortal Draw and which even Alekhine does not pass over in his own collection. Similarly some game collections of Tal’s are deprived of the fantastic draw against Aronin at the 24th Soviet championship (Moscow, 1957) – a game of which Keres stated in a much-acclaimed article that one could not do justice to Tal’s achievement in that tournament without coming to grips with it.’
(7049)
From Chess Panorama by William Lombardy and David Daniels (page 105):
‘Another way in which it is possible to annoy an opponent with impunity is to offer him a draw after every move. While it is true that the American master Arthur Dake was once forfeited against then world champion for repeatedly offering a draw, this is the only recorded instance, and it may well be doubted if the forfeit would have been imposed had the positions been reversed.’
Another instance of matter-of-fact fiction. Dake played Capa only once (when the Cuban was no longer champion), at New York, 1931. Hooper and Gilchrist’s book on Capablanca’s games remarks: ‘This was the only time that Capablanca won a lost endgame.’ An interview with Dake in the December 1984 Chess Life (page 30) shows that he simply threw away the game through a series of blunders/weak moves due to over-confidence.
(900)
It is possible that Lombardy and Daniels were thinking of the game between Dake and Turover at New York, 1931. John Rather (Kensington, MD, USA) supplies a copy of page 96 of the May-June 1931 American Chess Bulletin, which contains Alvin C. Cass’ adjudication of a dispute in which Dake was forfeited for distracting Turover in a time-scramble, although there was no question of persistent draw offers.
(1088)
Tartakower related an incident which occurred at Carlsbad, 1923:
‘… Teichmann, who did not like to overdo it, had accepted the draw offered by Réti when the tournament director, Mr Tietz, who considered that Teichmann had the better position and who “had his interests at heart”, refused to accept the decision and ordered the battle to continue. Teichmann then went for outright simplification … and soon sank. Was such a result not unfair?’
Source: Les Cahiers de l’Echiquier Français, issue 24, pages 244-245.
(2465)
At Bournemouth, 1939 Gerald Abrahams finished last with a single point, derived from a long win (available in various databases) against Mieses in the second round. CHESS, October 1939 (page 3) reported that during the game Mieses refused a draw five times. Do readers know of comparable cases of multiple refusals?
(3739)
Cases of an early agreement to a draw were discussed in C.Ns. 8162, 8167 and 8169.
C.N. 2549 (see page 359 of A Chess Omnibus) quoted this remark on Rubinstein by L. Steiner on page 54 of the March 1961 Chess World:
A claim about Emanuel Lasker’s practice appeared in ‘My Encounters with Lasker’ by Ossip Bernstein on pages 202-204 of the July 1955 Chess Review:
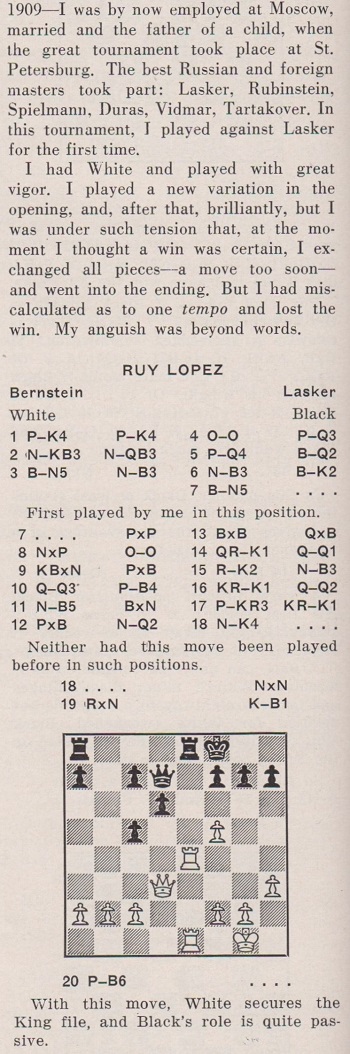
When was the term ‘grandmaster draw’ coined? On the first page of the Introduction to his book Prague 1946 (Sutton Coldfield, circa 1951) H. Golombek wrote: ‘the number of so-called “grandmaster draws” can be counted on the fingers of one hand.’ How much further back can the phrase be traced?
Below is an inscription by Golombek in our copy of Prague 1946 to the Czech master Jaroslav Šajtar:
(3803)
We have found some occurrences of ‘grandmaster draw’ from 1948 (i.e. a couple of years before FIDE officially brought in the title ‘grandmaster’).
In a report on the world championship match-tournament page 11 of the May 1948 Chess Review had two instances:
‘Round eight produced the first “grandmaster draw” of the tourney. On the 24th move, Keres proposed a draw and Reshevsky accepted.’
‘Many people feel that the “grandmaster draw” is the bane of competitive play.’
From page 308 of the September 1948 BCM (a report by H. Golombek on the Stockholm Interzonal tournament):
‘The Lilienthal-Bronstein game was a typical example of the so-called “grandmaster” draw.’
(6638)
One of the best illustrations we know of the need for eternal vigilance. White coasts along contentedly towards a grandmaster draw until ...
František Zita – Klaus Junge
Prague, 7 December 1942
King’s Indian Defence
1 c4 Nf6 2 Nf3 g6 3 g3 Bg7 4 Bg2 O-O 5 O-O d6 6 d4 Nc6 7 Nc3 e5 8 dxe5 dxe5 9 Qxd8 Rxd8 10 Bg5 Be6 11 Bxf6 Bxf6 12 Ne4 Be7 13 b3 f6 14 Rfd1 Rxd1+ 15 Rxd1 Rd8 16 Rxd8+ Nxd8 17 Ne1 f5 18 White resigns. He loses a piece.
Source: tournament book by Lachaga, page 14.
(689)
Wanted: nominations concerning lengthy matches devoid of draws.
The best-known case may be Steinitz’s defeat of Anderssen (+8 –6 =0) in London in 1866. Twenty years later, also in London, there was a tied contest between Bird and Burn in which all 18 games were decisive. Detailed coverage can be found in the McFarland monographs on the two players, by Hans Renette and Richard Forster respectively. This chart is on page 200 of the latter work:
(10220)
‘Schach in seiner gegenwärtigen Gestalt wird bald den Tod des Remis erleiden’, wrote Emanuel Lasker in his booklet Mein Wettkampf mit Capablanca (see pages 32-33 of the 1926 edition). The English translation on page 249 of the July 1921 BCM was: ‘Chess in its present form will die the death of the draw.’
For some comments by Capablanca, made while he was still world champion, see Capablanca on Moscow, 1925, as well as C.N. 4228. The latter item reproduced a remark by him written on 15 November 1925:
‘Chess is becoming so easy to play that very soon there will be several unbeatable players.’
It may be wondered when the Cuban first formed such a view, and one oddity, currently inexplicable to us, is a letter from C.Y.C. Dawbarn of Liverpool on pages 184-185 of the May 1922 BCM. It began:
‘In the course of his match with Dr Lasker, Señor Capablanca hazarded the opinion that chess was in fact exhausted; that, as in billiards or croquet, other reasons rather than the game itself determined the issue ...’
For his part, Capablanca stated a couple of months later:
‘I have been quoted as saying that chess has reached its limit. I never said anything of the kind. Somebody else made some such remark, and even he was misquoted.’
Source: The Times, 19 July 1922, page 15.
Page 177 of the December 1922 American Chess Bulletin
(5437)
A rare instance of perpetual check administered by two bishops:
P. Gaspary – N.N.
Athens, 1908
King’s Gambit Declined
14 Qe4 Qe8 15 Qxd5+ Be6 16 Bc4 (Gaspary endowed this move with an exclamation mark, commenting that after 16 Qxb7 Black would save the game with 16…Nd7. He did not mention 16 Qe4, which should probably have given him an easy win.) 16…Bxd5 17 Bxd5+ Kh7 18 Be4+ Kg8 19 Bd5+ Drawn.
Source: La Stratégie, November 1908, pages 392-393.
(2645)
The position below comes from page 68 of Schach by H. Ranneforth (Leipzig, 1936), which merely states that White was A. Jülich and that the game was played in 1906:
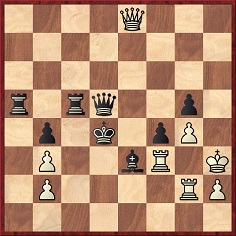
Play is said to have gone 1 Rd2+ Bxd2 2 Rd3+ Kxd3 3 Qe2+ Kd4 4 Qd3+ Ke5 5 Qf5+ Kd6 6 Qd7+ Drawn.
(2651)
C.N. 5647 gave an extract from The Pleasures of Chess by Assiac (New York, 1952):
1 e4 e5 2 Nf3 d6 3 d4 Nd7 4 Bc4 h6 5 dxe5 dxe5 6 Bxf7+ Kxf7 7 Nxe5+ Kf6 8 Qf3+ Kxe5 9 Qf7 Ngf6 10 Nd2 Qe8 11 Nc4+ Kxe4 12 f3+
12...Kf5+ 13 Ne3+ Ke5 14 Nc4+ Kf5+ Drawn.
We have still found no other games which finished with, in Assiac’s term, ‘double-perpetual’.
Frederick S. Rhine (Park Ridge, IL, USA) recalls a passage from page 153 of Pollock Memories by F.F. Rowland (Dublin, 1899). The writer is Pollock.
‘But I should like to see a position which Mr Loyd told me he had constructed some years ago – or, at least, was constructing. It was a sort of problem in which both kings were in perpetual check, and neither could escape, nor could either side either win or lose the game. He called it “The Whirlpool”.’
Our correspondent asks whether more is known about Loyd’s construction.
Michael McDowell (Westcliff-on-sea, England) points out to us that the Pollock passage was quoted at the start of an article ‘Consecutive Checks Task’ by John Roycroft on pages 56-57 of the July-September 1976 issue of The Problemist. It seems that no information about a Loyd ‘whirlpool’ composition has been found, but on a similar theme we pick from Mr Roycroft’s rich article a study by E.B. Cook published in the Illustrated London News of 7 June 1856:
White to move and draw
Solution: 1 Bf7+ Kg4 2 Be6+ Kf4 3 Rf5+ Kg4+ 4 Re5+ Kf4 5 Rf5+.
(5957)
To the Chess Notes main page.
To the Archives for other feature articles.
Copyright: Edward Winter. All rights reserved.