Edward Winter
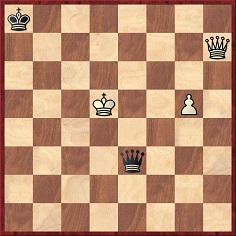
The March 1890 BCM (page 100) reported that ‘the following pretty ending occurred in a game recently played at the Vienna Club’.

White to move
White (Neumann) defeated an unnamed opponent with 1 Qe4 Qxg5+ 2 Kc6 ‘and Black cannot save mate. Had Black made any other move than taking the pawn, it will be seen that White equally wins.’
(1430)
From Ken Whyld (Caistor, England):
‘Readers may be puzzled to see that Neumann (who died in 1881) played a game “recently” in the 1890 BCM. It was not the Neumann but a Neumann; in fact Alexander Neumann (1856-1903). The original publication was in Österreichische Lesehalle, January 1887, page 31. The position is rotated, which affects variations using promotion. It is noted on page 123 (April) that what was in fact played was 1 Qd5 Qxb4+ 2 Kf3 Qe1 3 Qh5+ Kg1 4 Qg4+ Kf1 5 Qg2 mate, and that other replies would not have helped. Thus after 1...Qg6+ 2 Kf4+ Kh2 3 Qe5!, or 1 ...Qf6 2 Qh5+, followed by an exchange of queens, or 1...Qg3 2 b5.’
Michael Sharpe (Calgary, Canada) points out that this (rotated) position is also given on page 103 of The Tactics of End-Games by Jenő Bán (‘A. Neumann, 1887’) and page 144 of volume three of Lehr- und Handbuch der Endspiele by André Chéron (‘from a game by Neumann, 1887’).
The most detailed analysis we have found is on pages 75-76 of Johann Berger’s Theorie und Praxis der Endspiele, which acknowledges the Austrian journal as its source. P.W. Sergeant, in turn, credited Berger when using the position on pages 98-99 of An Introduction to the Endgame at Chess.
(1463)
A position published on page 27 of volume three of Comprehensive Chess Endings by Y. Averbakh, V. Henkin and V. Chekhover (Oxford, 1986)
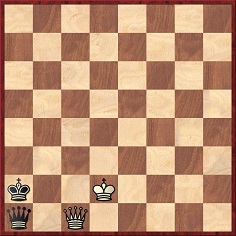
White to move
White wins by 1 Qc4+ Ka3 2 Qa6+ Kb2 3 Qb5+ Ka3 4 Qa5+ Kb2 5 Qb4+ and 6 Kc2.
No players are named, yet it is a mirror reflection of a position that arose in a game in the British Ladies’ Championship at Brighton in 1938 between Miss R.M. Dew and Mrs F.F. Thomson:
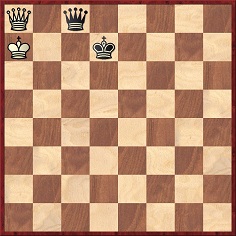
Black to move
CHESS (17 September 1928, page 21) reports:
‘A game in the Women’s Championship came down to the diagrammed position at adjournment-time and Mrs Thomson sealed the move ...Qc5+. Some bystanders audibly criticized Mrs Thomson for trying to win an obviously drawn game, so she changed her mind and accepted the draw. Subsequently, analysis revealed a forced win by Ka6 Qa3+; Kb7 Qb4+; Ka6 Qa4+; Kb7 Qb5+; Ka7 Kc7! and mates. Luckily this did not affect Mrs Thomson’s final position.’
An identical version of this incident is given on page 418 of the September 1938 BCM.
(1588)
As noted on page 50 of Chernev’s Wonders and Curiosities of Chess, N.M. MacLeod holds the unenviable record of the most games lost in a single tournament: 31 at New York, 1889.
He was, however, responsible for an extraordinary defeat of Emanuel Lasker in a simultaneous exhibition in Quebec in 1892. Extraordinary, because it must surely be the only game Lasker ever played in which he struggled on in vain when two queens down:
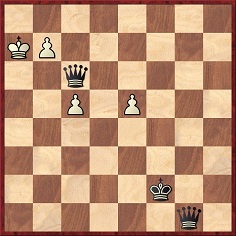
57....Qa1+ (There is a mate in two with 57...Qb1, 57...Qgh1 or 57...Qg7.) 58 Kb8 Qe8+ 59 Kc7 Qa5+ 60 Kd6 Qad8 mate.
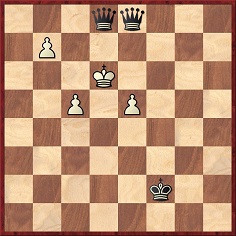
Source: BCM, August 1893, pages 359-360.
A potted biography of Nicholas Menelaus MacLeod which Jeremy Gaige sent us in 1983 was reproduced in C.N. 479 and is included in our feature article on Gaige.
Pages 77-80 of the Dresden, 1892 tournament book feature a remarkable game Albin-von Bardeleben in which six queens appear (not simultaneously). It is topped off with ‘a tragicomic final position’:
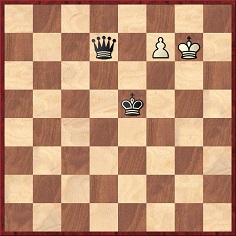
Instead of playing 92 Kh8, White blundered with 92 Kg8, which allows 92...Kf6 (inviting White to promote with check) 93 f8(Q)+ Kg6. White resigned, faced with a forced mate in three.
(751)
An endnote on page 257 of Chess Explorations:
C.N. 1217 noted that on page 8 of Chess: The Complete Self-Tutor Edward Lasker referred to a game with five queens ‘played in the international tournament of Karlsbad in 1911’, although ‘the fifth queen came off directly after promotion’. No such game is to be found in the tournament book, the closest being Burn-Chajes (four queens at one time, an exchange of one pair, and a fifth one later). As reported in C.N. 1395, N.I. Grekov mistakenly claimed that the Burn-Chajes game had ‘five queens on the board at the same time’ (CHESS, 14 October 1937, page 56).
Alekhine’s spurious five queens game against Grigoriev was featured in C.N.s 326 and 387. A comprehensive account of the game appeared in Chess Curiosities by T. Krabbé.
See too Chess Games with Five Queens.
Robert Timmer (Hilversum, the Netherlands) quotes positions where each side has two queens only:
Informator No. 35 (page 331) gave the ending of Bacsó v Szlabey, Hungary, 1983.
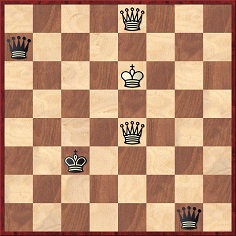
Play went: 1 Qh8+ Qad4 2 Qc8+ Qc5 3 Qe5+ Kb4 4 Qb2+ Ka5 5 Qa8+ Qa7 6 Qd5+ Resigns. [Addition on 28 July 2021: Modern computer programs confirm that White had a forced mate in all lines, contrary to the 1999 note by Richard Forster which was added when this C.N. item was reproduced on pages 23-24 of Kings, Commoners and Knaves.]
ii) A composition by Noam D. Elkies on page 58-59 of issue 2 of the American Chess Journal. In the summer of 1992 Lewis Stiller discovered a mutual Zugzwang position (White: king on h1 and queens on h2 and g2. Black: king on a1 and queens on a7 and f6) which Elkies used to create the following study:
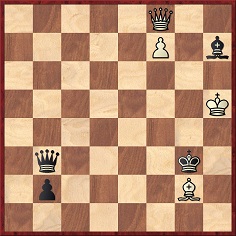
White to move and win
The bare bones of the solution: 1 Qg7+ Kh2 2 f8(Q) Qb5+ 3 Kh6 Qb6+ 4 Bc6 Qxc6+ 5 Kxh7 b1(Q)+ 6 Kh8 Kh1 7 Qfg8 and wins. This is the Stiller position, rotated by 90 degrees.
(2034)

Gustav Zeissl-Eduard Hamlisch, Vienna, 26 April 1899
Play continued: 1 Kd5 Kc3 2 c5 bxc5 3 Kxc5 Kd3 4 Kd5 Ke3 5 Ke5 Kf3 6 Kf5 Kg3 7 Kxg5 Kxh3 8 Kf4 Kg2 9 g5 h3 10 g6 h2 11 g7 h1(Q) 12 g8(Q)+ Kf1 13 Qc4+
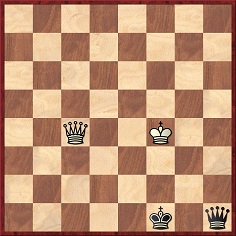
13…Kf2 14 Qc2+ Kf1 15 Qd1+ Kg2 16 Qe2+ Kg1 17 Kg3 and wins.
On page 19 of the January 1900 Wiener Schachzeitung Hamlisch pointed out that in the diagram above he could have drawn with 13…Kg1.
(2503)
In the position below, from a game played in Berlin, Alfred Sormann (Black, to move) agreed to a draw.
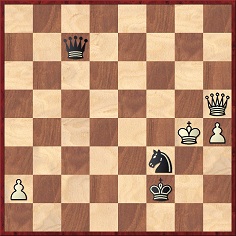
Ehrhardt Post and Berthold Lasker pointed out that he could have won his opponent’s queen or administered an artistic mate in 12 moves: 1…Qg3+ 2 Kf5 Qe5+ 3 Kg6 Qe8+ 4 Kh6 Qh8+ 5 Kg6 Nxh4+ 6 Kg5 Qe5+ 7 Kh6 Nf5+ 8 Kg6 Ne7+ 9 Kh6 Qh8+ 10 Kg5 Qg7+ 11 Kf4 Qg3+ 12 Ke4 Qe3 mate.
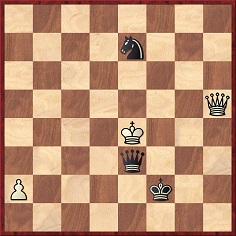
Source: Deutsches Wochenschach, 2 February 1908, page 45. The June 1908 issue of La Stratégie (page 191) erroneously presented this line as the actual conclusion to the game (also omitting the irrelevant pawn at a2), while the Study Database 2000 gives more or less the same position (with colours reversed) as being by Sormann (from an unknown 1908 source).
(2697)

A particularly interesting chapter in Practical Endgame Play – beyond the basics by Glenn Flear (London, 2007) is entitled ‘Queen and Bishop versus Queen and Knight’ (pages 422-454). From his introduction to the topic, on page 422:
‘... I don’t necessarily agree with the clichéd adage that “the queen and knight duo are superior”.
This thought-provoking comment is generally attributed to the great pre-war technical specialist Capablanca. Is it that he felt that the queen and knight form a complementary partnership, whereas the strengths of queen and bishop are outweighed by their lack of flexibility, or even their incompetence, on one colour complex? It’s an interesting opinion, nevertheless, and one that is worth developing; especially as in most simplified positions, ceteris paribus, the bishop is generally considered as a superior piece to the knight. Determining whether or not the great Cuban was right is far from easy; for example, I have found no Capablanca games that would support his assertion.’
As regards the Cuban’s specific statements on the subject, we reproduce below our overview in C.N. 2696 (see page 200 of A Chess Omnibus):
From Tim Bogan (Chicago, IL, USA):
‘In Chess Fundamentals, in a section headed Relative Value of the Pieces, Capablanca weighs the usefulness of bishop and knight in connection with other pieces and pawns, and states, in part:
‘A bishop and a rook are also stronger than a knight and a rook, but a queen and a knight may be stronger than a queen and a bishop.’ (my italics)
How did this become “Capablanca’s contention that queen and knight are superior to queen and bishop in the ending is very insightful” in Steve Mayer’s Bishop versus Knight: The Verdict (page 209)?’
After also referring to the discussion of this matter on page 350 of Fundamental Chess Endings by K. Müller and F. Lamprecht (who write, ‘Is Capablanca’s theorem that queen and knight are better than queen and bishop true?’) and Secrets of Modern Chess Strategy by J. Watson (pages 71-74), our correspondent asks:
‘Did Capablanca ever state his “theorem” as strongly as these later writers suggest?’
We are hovering, and havering, between ‘yes’, ‘no’, ‘perhaps’ and ‘don’t know’. On a subsequent occasion (i.e. a May 1932 lecture – see page 250 of our book on Capablanca) he did indeed dispense with the ‘may be’, declaring:
‘Queen and knight, however, are stronger than queen and bishop. The outcome of a game often depends on being able to obtain this combination. In pawn endings a bishop is preferable to a knight; however, in queen endings the knight is stronger.’
In the ‘Endgame Masters’ chapter of Capablanca’s Last Chess Lectures the fifth of nine ‘simple but valuable rules’ was also categorical: ‘Queen and knight are superior to queen and bishop.’
However, such statements do not necessarily refer to a confrontation between these forces. Indeed, it was when discussing a position in which Black had queen and knight and White had no minor pieces that Botvinnik wrote:
‘The queen and the knight together work miracles here. Capablanca was the first to point out the strength of these two pieces working together.’
Source: page 52 of Botvinnik on the Endgame (Coraopolis, 1985).
An historical remark in passing: to mention just one pre-Capablanca book at random, in The Art of Chess (London, 1895) James Mason noted (pages 92-94) that the ending queen and bishop versus queen was usually drawn, whereas queen and knight versus queen was frequently a win.
On the substantive issue, therefore, our tentative conclusion is that whereas some present-day writers have examined Capablanca’s ‘theorem’ in terms of queen and knight versus queen and bishop, the Cuban was more likely merely expounding (though not inventing) a general preference for the queen to be accompanied by a knight rather than by a bishop, regardless of what material the opponent held.
(5748)
To the Chess Notes main page.
To the Archives for other feature articles.
Copyright: Edward Winter. All rights reserved.